题目内容
12.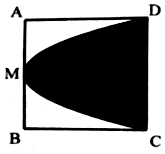 如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )
如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{2}$ | D. | $\frac{8}{3}$ |
分析 由题意,建立如图所示的坐标系,求出抛物线的方程,利用定积分求面积即可.
解答  解:由题意,建立如图所示的坐标系,则D(2,1),
解:由题意,建立如图所示的坐标系,则D(2,1),
设抛物线方程为y2=2px,代入D,可得p=$\frac{1}{4}$,∴y=$\sqrt{\frac{1}{2}x}$,
∴S=$2{∫}_{0}^{2}\sqrt{\frac{1}{2}x}dx$=$\sqrt{2}•\frac{2}{3}{x}^{\frac{3}{2}}$${|}_{0}^{2}$=$\frac{8}{3}$,
故选D.
点评 本题考查利用定积分求面积,考查学生的计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.已知抛物线C:y2=8x,直线l:y=$\frac{{\sqrt{3}}}{3}$(x-2),直线l交C于A,B两点,则|AB|等于( )
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
20.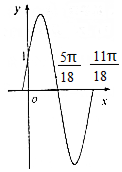 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
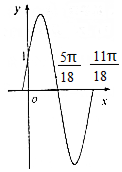 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
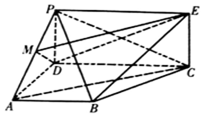 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.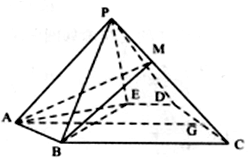 如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.
如图,在五棱锥P-ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.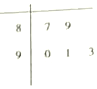 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )