题目内容
已知函数f（x）=2x2-kx+1在区间[1，3]上是增函数，则实数k的取值范围为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：对称轴为x=
，函数f（x）=2x2-kx+1在区间[1，3]上是增函数，
≤1，求解即可．
| k |
| 4 |
| k |
| 4 |
解答：
解：∵函数f（x）=2x2-kx+1
∴对称轴为x=
∵函数f（x）=2x2-kx+1在区间[1，3]上是增函数，
∴
≤1
即k≤4
故答案为：（-∞，4]
∴对称轴为x=
| k |
| 4 |
∵函数f（x）=2x2-kx+1在区间[1，3]上是增函数，
∴
| k |
| 4 |
即k≤4
故答案为：（-∞，4]
点评：本题考查了二次函数的单调性，对称性，难度不大，属于容易题，关键是确定对称轴．
练习册系列答案
科学实验活动册系列答案
相关题目
i是虚数单位，
的共轭复数为（ ）
| 2i |
| 1+i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
过抛物线y2=4x焦点作直线L与抛物线交于A、B，过A、B分别作抛物线的切线交于点P，则△ABP为（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、随P位置变化前三种情况都有可能 |
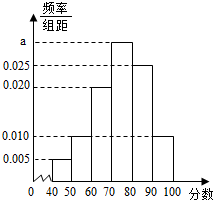为了更好的了解某校高三学生期中考试的数学成绩情况，从所有高三学生中抽取40名学生，将他们的数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…，[90，100]后得到如图所示的频率分布直方图．