题目内容
设 是奇函数,且
是奇函数,且 时,
时, ,则
,则 _________.
_________.
 .
.
【解析】
试题分析:因为 是奇函数,所以
是奇函数,所以 ,即
,即 ,
,
则 .
.
考点:函数的性质与求值.

练习册系列答案
相关题目
(本题12分) 某县教研室要分析学生初中升学的数学成绩对高一年级数学成绩有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末成绩y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)计算入学成绩 与高一期末成绩
与高一期末成绩 的相关系数;
的相关系数;
(2)对变量 与
与 进行相关性检验,如果
进行相关性检验,如果 与
与 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
(本题满分12分) 某企业常年生产一种出口产品,根据预测可知,进入2l世纪以来,该产品的产量平稳增长.记2008年为第1年,且前4年中,第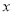 年与年产量
年与年产量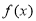 (万件)之间的关系如下表所示:
(万件)之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 4.00 | 5.58 | 7.00 | 8.44 |
若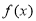 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一: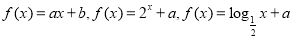 .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取08年和10年的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2014年的年产量比预计减少30%,试根据所建立的函数模型,确定2014年的年产量.
 ,公比不等于
,公比不等于 的等比数列
的等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列. 的通项公式;
的通项公式; ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
 .
.
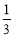
 C.
C.

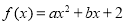 是定义在
是定义在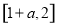 上的偶函数,则
上的偶函数,则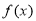 的值域是
的值域是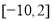 B.
B.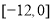
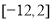 D.与
D.与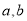 有关,不能确定
有关,不能确定 ,经过
,经过 天后体积与天数
天后体积与天数 的关系式为:
的关系式为: ,若新丸经过50天后,体积变为
,若新丸经过50天后,体积变为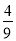
 ;若一个新丸体积变为
;若一个新丸体积变为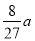 ,则需经过的天数为
,则需经过的天数为 是偶函数,其定义域为
是偶函数,其定义域为 ,且在
,且在 上是减函数,则
上是减函数,则 的大小关系是
的大小关系是 >
> B.
B. <
<


 D.
D.


 (y≠0) (B)
(y≠0) (B) (y≠0)
(y≠0) (y≠0) (D)
(y≠0) (D) (y≠0)
(y≠0)