题目内容
(本小题满分14分)
已知首项为 ,公比不等于
,公比不等于 的等比数列
的等比数列 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证:
 .
.
(1) ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)由 ,
, ,
, 成等差数列,得
成等差数列,得 ,转化可得
,转化可得 ,即可得数列
,即可得数列 的通项公式;(2)先用错位相减法求出
的通项公式;(2)先用错位相减法求出 ,再算出
,再算出 ,即可比较
,即可比较 与
与 的大小关系.
的大小关系.
试题解析:(1)【解析】
由题意得 , 1分
, 1分
即 ,
,
即 . 2分
. 2分
∴  . 3分
. 3分
∴ 公比 . 4分
. 4分
∴  . 5分
. 5分
另解:由题意得 ,
, , 1分
, 1分
∴ . 2分
. 2分
化简得 ,解得
,解得 , 4分
, 4分
∴ . 5分
. 5分
(2)【解析】 , 6分
, 6分
∴  , ① 7分
, ① 7分
 , ② 8分
, ② 8分
① ②得,
②得,

 10分
10分
∴  . 12分
. 12分
∴  . 14分
. 14分
考点:1、等比数列的通项公式;2、等差数列的性质;3、数列求和.

 与椭圆
与椭圆 的公共点,用线段连接起来所得到的图形
的公共点,用线段连接起来所得到的图形 的各项和等于公比
的各项和等于公比 ,则首项
,则首项 的最大值是 .
的最大值是 . 若
若 ,则实数t的取值范围是
,则实数t的取值范围是 B.
B. C.
C. D.
D.
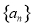 的公比为2,若
的公比为2,若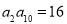 ,则
,则 的值是
的值是 的直径
的直径 ,直线
,直线 与圆
与圆 相切于点
相切于点 ,
, 于点D,若
于点D,若 ,设
,设 ,则
,则 ______.
______.
 ,
, ,
, 表示空间中三条不同的直线,
表示空间中三条不同的直线,  表示平面, 给出下列命题:
表示平面, 给出下列命题: ,
,  , 则
, 则 ∥
∥ ; ② 若
; ② 若 ,
,  ∥
∥ ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ; ④ 若
; ④ 若

 中,设不等式组
中,设不等式组 所表示的平面区域是
所表示的平面区域是 ,从区域
,从区域 中随
中随 ,则
,则 的概率是 .
的概率是 . 是奇函数,且
是奇函数,且 时,
时, ,则
,则 _________.
_________.