题目内容
5.已知e为自然对数的底数,函数f(x)=$\left\{\begin{array}{l}{4x-4,x≤0}\\{{e}^{x},x>0}\end{array}\right.$,则方程f(x)=ax恰有两个不同的实数解时,实数a的取值范围是( )| A. | (e,4] | B. | (4,+∞) | C. | (e,+∞) | D. | ($\frac{1}{e}$,4) |
分析 作出函数f(x)的图象,利用数形结合结合导数求出函数的切线斜率,即可得到结论.
解答 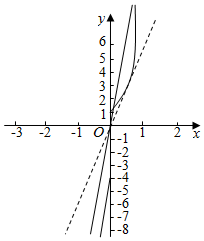 解作出函数f(x)的图象如图,
解作出函数f(x)的图象如图,
设y=kx与f(x)=ex,在x>0相切时,设切点为P(m,n),
则函数的导数f′(x)=ex,
则在P(m,n)处的切线斜率k=f′(m)=em,
则切线方程为y-n=em(x-m),
即y=emx+em-mem,
当x=0,y=0时,em-mem=0,
即1-m=0,m=1,此时切线斜率k=f′(m)=e,
∵e<4,
∴当a=e时,直线y=ex与f(x)只有一个交点,
当a>e时,在x>0上,f(x)与y=ax有两个交点,
当a=4时,y=ax与y=4x-4,平时,此时f(x)与y=ax有两个交点,
当a>4时,此时f(x)与y=ax有3个交点,
综上若f(x)=ax恰有两个不同的实数解时,
则e<a≤4,
故选:A
点评 本题主要考查函数与方程的应用,作出函数f(x),利用数形结合是解决本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
17.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),若(k$\overrightarrow{a}+\overrightarrow{b}$)⊥(3$\overrightarrow{a}-\overrightarrow{b}$),则实数k=( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
14.执行如图所示的程序框图,则下列说法正确的( )
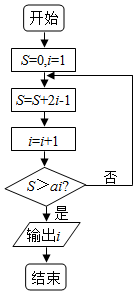

| A. | ?a∈(2,4),输出的i的值为5 | B. | ?a∈(4,5),输出的i的值为5 | ||
| C. | ?a∈(3,4),输出的i的值为5 | D. | ?a∈(2,4),输出的i的值为5 |
14.如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )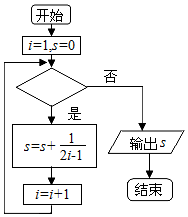

| A. | i≤1008? | B. | i>1008? | C. | i≤1009? | D. | i>1009? |
 如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.