题目内容
如要在下表所示的3×3正方形的9个空格中填入正整数,使得每行都成等差数列,每一列都成等比数列,则标有*号的空格应填的正整数是
| 1 | 3 | |
| * | 12 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据等比中项和等差中项的性质分别求出未知的项即可得到结论.
解答:
解:设对应的未知数值分布用字母表示:
第一行根据等差数列的性质可知中间数c=
=
=2,
根据等比数列的性质可知第三列中间的数f=
=
=6,
标有*号的空格应填的正整数a,则第三行第二个数为e=
,
b=
,d=
,
则c,d,e成等比数列,
∴
×2=(
)2,
解得a=4,
故标有*号的空格应填的正整数是4,
故答案为:4.
| 1 | c,(c=2) | 3 |
| b | d | f,(f=6) |
| a | e | 12 |
| 1+3 |
| 2 |
| 4 |
| 2 |
根据等比数列的性质可知第三列中间的数f=
| 3×12 |
| 36 |
标有*号的空格应填的正整数a,则第三行第二个数为e=
| a+12 |
| 2 |
b=
| a |
| ||
| 2 |
则c,d,e成等比数列,
∴
| a+12 |
| 2 |
| ||
| 2 |
解得a=4,
故标有*号的空格应填的正整数是4,
故答案为:4.
点评:本题主要考查等比数列和等差数列的性质,利用等比中项和等差中项的定义和性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
计算cos330°的值为( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
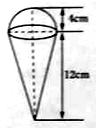 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π≈3.14) 一正棱柱其三视图如图所示,该正多面体的体积为
一正棱柱其三视图如图所示,该正多面体的体积为
 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的表面积是
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的表面积是