题目内容
15.设函数f(x)=(x-1)2+blnx,其中b为常数,讨论函数f(x)在定义域上的单调性.分析 先求出函数的导数,通过讨论b的范围,从而求出函数的单调区间,进而求出函数的极值点.
解答 解:f(x)=(x-1)2+blnx,(x>0),
∴f′(x)=2(x-1)+$\frac{b}{x}$=$\frac{2(x-\frac{1}{2})^{2}+b-\frac{1}{2}}{x}$,
①b-$\frac{1}{2}$≥0即b≥$\frac{1}{2}$时,f′(x)≥0,f(x)在(0,+∞)单调递增,
∴函数f(x)无极值点;
②b<$\frac{1}{2}$时,令f′(x)=0,解得:x=$\frac{1±\sqrt{1-2b}}{2}$,
0<b<$\frac{1}{2}$时:
在(0,$\frac{1-\sqrt{1-2b}}{2}$),($\frac{1+\sqrt{1-2b}}{2}$,+∞),f′(x)>0,f(x)递增,
在($\frac{1-\sqrt{1-2b}}{2}$,$\frac{1+\sqrt{1-2b}}{2}$),f′(x)<0,f(x)递减,
当b≤0时,$\frac{1-\sqrt{1-2b}}{2}$<0,
在($\frac{1+\sqrt{1-2b}}{2}$,+∞),f′(x)>0,f(x)递增,
在(0,$\frac{1+\sqrt{1-2b}}{2}$),f′(x)<0,f(x)递减.
点评 本题考查了函数的单调性,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
7.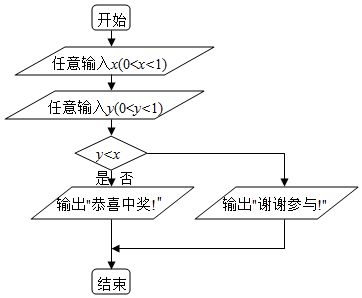 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
 在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图所示程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
3.若sinα+cosα=tan390°,则sin2α等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
20.下列关于命题的说法中错误的是( )
| A. | 对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1≥0 | |
| B. | “x=1”是“x2-4x+3=0”的充分不必要条件 | |
| C. | 命题“若x2-4x+3=0,则x=1”的逆否命题为“若x≠1,则x2-4x+3≠0” | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
7.已知a,b∈R+,且直线ax+by-6=0与直线2x+(b-3)y+5=0互相平行,则2a+3b的最小值为( )
| A. | 12 | B. | 25 | C. | $13+2\sqrt{6}$ | D. | $12+4\sqrt{3}$ |
4.三棱锥的三条侧棱两两垂直,其长分别为$\sqrt{3},\sqrt{2},1$,则该三棱锥的外接球的表面积( )
| A. | 24π | B. | 18π | C. | 10π | D. | 6π |
5.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是( )
| A. | (6,+∞) | B. | [6,+∞) | C. | (3,+∞) | D. | [3,+∞) |