题目内容
7.已知a,b∈R+,且直线ax+by-6=0与直线2x+(b-3)y+5=0互相平行,则2a+3b的最小值为( )| A. | 12 | B. | 25 | C. | $13+2\sqrt{6}$ | D. | $12+4\sqrt{3}$ |
分析 由两直线平行的条件得到$\frac{2}{a}+\frac{3}{b}$=1,由2a+3b=(2a+3b)($\frac{2}{a}+\frac{3}{b}$)展开后利用基本不等式求得最值.
解答 解:∵直线ax+by-6=0与直线2x+(b-3)y+5=0互相平行,
∴a(b-3)-2b=0且5a+12≠0,
∴3a+2b=ab,即$\frac{2}{a}+\frac{3}{b}$=1,
又a,b均为正数,
则2a+3b=(2a+3b)($\frac{2}{a}+\frac{3}{b}$)=4+9+$\frac{6a}{b}$+$\frac{6b}{a}$≥13+12=25.
当且仅当a=b=5时上式等号成立.
故选:B.
点评 本题考查了直线的一般式方程与直线平行的关系,训练了利用基本不等式求最值,是基础题.

练习册系列答案
相关题目
2.一个盒子中共有12个大小相同的小球,其中红球9个,黄球3个,从盒子中任取3个球,将其中的红球染成黄色连同黄球一起放回,此时盒子中黄球的个数为ξ,则Eξ=( )
| A. | 1 | B. | $\frac{21}{4}$ | C. | $\frac{17}{4}$ | D. | 3 |
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线过圆Q:x2+y2-4x+6y=0的圆心,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{13}}{3}$ | D. | 3 |
16.已知双曲线的焦点分别为(0,-2)、(0,2),且经过点P(-3,2),则双曲线的标准方程是( )
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
17.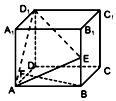 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )| A. | 平行 | B. | 相交但不垂直 | C. | 垂直 | D. | 异面 |
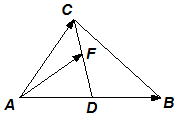 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.