题目内容
3.若sinα+cosα=tan390°,则sin2α等于( )| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 两边平方,利用同角三角函数基本关系式,二倍角的正弦函数公式,诱导公式,特殊角的三角函数值可得:1+sin2α=tan230°=$\frac{1}{3}$,进而可求sin2α的值.
解答 解:∵sinα+cosα=tan390°,
∴两边平方,可得:1+sin2α=tan230°=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$,
∴解得:sin2α=-$\frac{2}{3}$.
故选:A.
点评 本题主要考查了同角三角函数基本关系式,二倍角的正弦函数公式,诱导公式,特殊角的三角函数值在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线过圆Q:x2+y2-4x+6y=0的圆心,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{13}}{3}$ | D. | 3 |
13.一个直三棱柱的每条棱长都是4$\sqrt{3}$,且每个顶点都在球O的球面上,则球O的表面积为( )
| A. | 84π | B. | 96π | C. | 112π | D. | 144π |
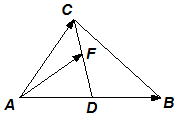 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}$+$\frac{4}{y+1}$的最小值为3+2$\sqrt{2}$.