题目内容
5.设抛物线的焦点到顶点的距离为3,则抛物线上的点到准线的距离的取值范围是( )| A. | (6,+∞) | B. | [6,+∞) | C. | (3,+∞) | D. | [3,+∞) |
分析 直接利用抛物线的性质写出结果即可.
解答 解:抛物线的焦点到顶点的距离为3,
可得$\frac{P}{2}$=3,则抛物线上的点到准线的距离的取值范围是:[3,+∞).
故选:D.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知双曲线的焦点分别为(0,-2)、(0,2),且经过点P(-3,2),则双曲线的标准方程是( )
| A. | $\frac{x^2}{3}-{y^2}$=1 | B. | $\frac{y^2}{3}-{x^2}$=1 | C. | y2-$\frac{x^2}{3}$=1 | D. | $\frac{x^2}{2}-\frac{y^2}{2}$=1 |
13.一个直三棱柱的每条棱长都是4$\sqrt{3}$,且每个顶点都在球O的球面上,则球O的表面积为( )
| A. | 84π | B. | 96π | C. | 112π | D. | 144π |
17.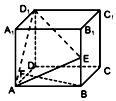 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
 在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )
在如图所示的正四棱柱ABCD-A1B1C1D1中,E、F分别是棱B1B、AD的中点,直线BF与平面AD1E的位置关系是( )| A. | 平行 | B. | 相交但不垂直 | C. | 垂直 | D. | 异面 |
14.下列四个命题中是真命题的是( )
| A. | x>3是x>5的充分条件 | B. | x2=1是x=1的充分条件 | ||
| C. | a>b是ac2>bc2的必要条件 | D. | $α=\frac{π}{2}是sinα=1的必要条件$ |
15.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-x2+1 | B. | y=x-2 | C. | y=log2x | D. | y=($\frac{1}{2}$)x |
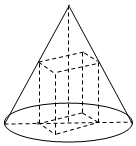 底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为3,高为$6\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).