题目内容
20.函数$f(x)={log_{\frac{1}{2}}}x$的递减区间是( )| A. | $(0,\frac{1}{2}]$ | B. | (0,+∞) | C. | (0,1] | D. | [1,+∞) |
分析 根据对数函数的性质判断函数的单调性即可.
解答 解:0<$\frac{1}{2}$<1,
故函数f(x)在(0,+∞)递减,
故选:B.
点评 本题考查了对数函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
11.已知P是直线kx+4y-10=0(k>0)上的动点,是圆C:x2+y2-2x+4y+4=0的两条切线,A,B是切点,C是圆心,若四边形PACB面积的最小值为$2\sqrt{2}$,则k的值为( )
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{15}{2}$ |
12.若某产品的直径长与标准值的差的绝对值不超过1mm时,则视为合格品,否则视为不合格品.在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽样5000件进行检测,结果发现有50件不合格.计算这50件不合格的直径长与标准值的差(单位:mm),将所得数据进行分组,得出频率分布表如下:
(1)表格①②③④缺少的数据分别是什么?
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在(1,3]内的概率;
(3)现对该厂这种产品的某批次进行检查,结果发现有20件产品不合格,据此估算这批产品中合格品的件数.
| 分组 | 频数 | 频率 |
| [-3,-2) | ① | 0.10 |
| [-2,-1) | 8 | 0.16 |
| (1,2] | ② | 0.50 |
| (2,3] | 10 | ③ |
| (3,4] | ④ | 0.04 |
| 合计 | 50 | 1.00 |
(2)估计该厂生产的此种产品中,不合格的直径长与标准值的差落在(1,3]内的概率;
(3)现对该厂这种产品的某批次进行检查,结果发现有20件产品不合格,据此估算这批产品中合格品的件数.
16.如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log3(x+1)的解集是( )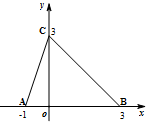

| A. | {x|-1≤x≤2} | B. | {x|-1<x≤2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤3} |