题目内容
20．用1，2，3，4，5组成不含重复数字的五位数，要求数字4不出现在首位和末位，数字1，3，5中有且仅有两个数字相邻，则满足条件的不同五位数的个数是48．（注：结果请用数字作答）分析 对数字4分类讨论，结合数字1，3，5中有且仅有两个数字相邻，利用分类计数原理，即可得出结论．
解答 解：数字4出现在第2位时，数字1，3，5中相邻的数字出现在第3，4位或者4，5位，共有C32A22A22=12个，
数字2出现在第4位时，同理也有12个；
数字4出现在第3位时，数字1，3，5中相邻的数字出现在第1，2位或第4，5位，共有C21C32A22A22=24个，
故满足条件的不同五位数的个数是48．
故答案为：48．
点评 本题考查分类计数原理，考查排列、组合知识，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
12．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{x-2y+2≥0}\end{array}\right.$则z=$\frac{y}{x-3}$的最小值等于（ ）
| A． | -4 | B． | -2 | C． | -$\frac{1}{8}$ | D． | 0 |
15．已知函数f（x）=f'（1）x2+x+1，则$\int_0^1{f（x）}dx$=（ ）
| A． | $-\frac{7}{6}$ | B． | $\frac{7}{6}$ | C． | $\frac{5}{6}$ | D． | $-\frac{5}{6}$ |
5．已知对任意实数x．都有f（-x）=-f（x），g（-x）=g（x），且x＞0时，f′（x）＞0，g′（-x）＞0，则x＜0时有（ ）
| A． | f′（x）＞0，g′（-x）＞0 | B． | f′（x）＞0，g′（-x）＜0 | C． | f′（x）＜0，g′（-x）＞0 | D． | f′（x）＜0，g′（-x）＜0 |
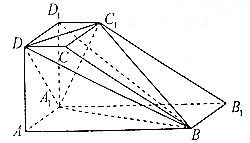如图，直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形，其中AB⊥AD，AB=2AD=2AA1=4，CD=1．