题目内容
19.已知函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)与g(x)=2cos(2x+φ)-1的图象有相同的对称轴,若$x∈[0,\frac{π}{2}]$,则f(x)的取值范围是( )| A. | $(-\frac{3}{2},3)$ | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},\frac{3}{2}]$ | D. | [-3,3] |
分析 根据函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)与g(x)=2cos(2x+φ)-1的图象有相同的对称轴,其周期T相同,可得ω=2,$x∈[0,\frac{π}{2}]$,求出2x-$\frac{π}{6}$的范围,结合三角函数的图象及性质可知f(x)的取值范围.
解答 解:由题意,函数f(x)=3sin(ωx-$\frac{π}{6}$)(ω>0)与g(x)=2cos(2x+φ)-1的图象有相同的对称轴,其周期T相同,∴ω=2.
可得f(x)=3sin(2x-$\frac{π}{6}$),
当$x∈[0,\frac{π}{2}]$时,则2x-$\frac{π}{6}$∈[$-\frac{π}{6}$,$\frac{5π}{6}$],
当2x-$\frac{π}{6}$=$-\frac{π}{6}$时,函数f(x)取得最小值为$-\frac{1}{2}×3=-\frac{3}{2}$,
当2x-$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为1×3=3,
∴f(x)的取值范围是[$-\frac{3}{2}$,3];
故选:B
点评 本题主要考擦周期的问题和对称轴的关系.确定其解析式是哦关键,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
17.若点A$(\frac{π}{6},0)$、$B(\frac{π}{3},0)$是函数y=f(x)=sin(ωx+φ)的两个相邻零点,则$f(-\frac{π}{3})$=( )
| A. | -1 | B. | 1 | C. | 0 | D. | $\frac{1}{2}$ |
4.$f(x)=\sqrt{2}sin({x+φ})-a+{e^{-x}}$,$φ∈({0,\frac{π}{2}})$,已知f(x)的图象在(0,f(0))处的切线与x轴平行或重合.
(1)求φ的值;
(2)若对?x≥0,f(x)≤0恒成立,求a的取值范围;
(3)利用如表数据证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}<106}$.
(1)求φ的值;
(2)若对?x≥0,f(x)≤0恒成立,求a的取值范围;
(3)利用如表数据证明:$\sum_{k=1}^{157}{sin\frac{kπ}{314}<106}$.
| ${e^{\frac{π}{314}}}$ | ${e^{-\frac{π}{314}}}$ | ${e^{\frac{78π}{314}}}$ | ${e^{-\frac{78π}{314}}}$ | ${e^{\frac{79π}{314}}}$ | ${e^{-\frac{79π}{314}}}$ |
| 1.010 | 0.990 | 2.182 | 0.458 | 2.204 | 0.454 |
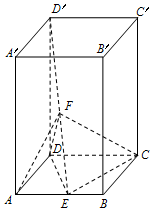 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.