题目内容
已知双曲线中心在原点,且一个焦点为(
,0),直线y=x-1与其相交于M,N两点,MN的中点的横坐标为-
,求此双曲线的方程.
| 7 |
| 2 |
| 3 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:先设出双曲线的方程,然后与直线方程联立方程组,经消元得二元一次方程,再根据韦达定理及MN的中点的横坐标为-
,即得双曲线方程.
| 2 |
| 3 |
解答:
解 设双曲线方程为
-
=1(a>0,b>0),依题意c=
,
∴方程可以化为
-
=1,
由直线代入得(7-2a2)x2+2a2x-8a2+a4=0.
设M(x1,y1),N(x2,y2),则x1+x2=
,
∵MN的中点的横坐标为-
,
∴
×
=-
,解得a2=2,
∴双曲线的方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
∴方程可以化为
| x2 |
| a2 |
| y2 |
| 7-a2 |
由直线代入得(7-2a2)x2+2a2x-8a2+a4=0.
设M(x1,y1),N(x2,y2),则x1+x2=
| -2a2 |
| 7-2a2 |
∵MN的中点的横坐标为-
| 2 |
| 3 |
∴
| 1 |
| 2 |
| -2a2 |
| 7-2a2 |
| 2 |
| 3 |
∴双曲线的方程为
| x2 |
| 2 |
| y2 |
| 5 |
点评:本题主要考查代数方法解决几何问题,同时考查双曲线的标准方程与性质等.

练习册系列答案
相关题目
已知命题p:x2+2x-3>0;命题q:x>a,且?q的一个充分不必要条件是?p,则实数a的取值范围是( )
| A、(-∞,1] |
| B、(-∞,-3] |
| C、[-1,+∞) |
| D、[1,+∞) |
函数f(x)=x2-2lnx的单调减区间是( )
| A、(0,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-1,1) |
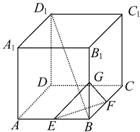 在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )