题目内容
已知函数f(x)=x3-2ax2+bx+c,
(1)当c=0时,f(x)在点P(1,3)处的切线平行于直线y=x+2,求a,b的值;
(2)若f(x)在点A(-1,8),B(3,-24)处有极值,求f(x)的表达式.
(1)当c=0时,f(x)在点P(1,3)处的切线平行于直线y=x+2,求a,b的值;
(2)若f(x)在点A(-1,8),B(3,-24)处有极值,求f(x)的表达式.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求出原函数的导函数,利用f(1)=3,f′(1)=1联立方程组求解a,b的值;
(2)由f(x)在点A(-1,8),B(3,-24)处有极值,得到f′(-1)=f′(3)=0,结合f(1)=8求解a,b,c的值,验证f(3)=-24得答案.
(2)由f(x)在点A(-1,8),B(3,-24)处有极值,得到f′(-1)=f′(3)=0,结合f(1)=8求解a,b,c的值,验证f(3)=-24得答案.
解答:
解:(1)当c=0时,f(x)=x3-2ax2+bx.
∴f′(x)=3x2-4ax+b.
依题意可得f(1)=3,f′(1)=1,
即
,解得
;
(2)由f(x)=x3-2ax2+bx+c,
得f′(x)=3x2-4ax+b.
令
,解得
,
由f(-1)=-1-2a-b+c=8,a=
,b=-9,可得c=3.
∴f(x)=x3-3x2-9x+3.
检验知f(3)=33-3×32-9×3+3=-24符合题意.
∴f(x)=x3-3x2-9x+3.
∴f′(x)=3x2-4ax+b.
依题意可得f(1)=3,f′(1)=1,
即
|
|
(2)由f(x)=x3-2ax2+bx+c,
得f′(x)=3x2-4ax+b.
令
|
|
由f(-1)=-1-2a-b+c=8,a=
| 3 |
| 2 |
∴f(x)=x3-3x2-9x+3.
检验知f(3)=33-3×32-9×3+3=-24符合题意.
∴f(x)=x3-3x2-9x+3.
点评:本题考查利用导数研究曲线上某点处的切线方程,解答此题的关键是注意极值点处的导数等于0,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
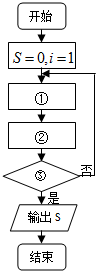 画出一个计算1+
画出一个计算1+