题目内容
已知x，y，z均为正数，且x+y+z=2，则
+
+
的最大值是（ ）
| x |
| 2y |
| 3z |
| A、2 | ||
B、2
| ||
C、2
| ||
| D、?3 |
考点：二维形式的柯西不等式
专题：计算题,不等式的解法及应用
分析：利用柯西不等式，可得（1+2+3）（x+y+z）≥（
+
+
）2，结合x+y+z=2，即可求出
+
+
的最大值．
| x |
| 2y |
| 3z |
| x |
| 2y |
| 3z |
解答：
解：∵x、y、z是正数，
∴（1+2+3）（x+y+z）≥（
+
+
）2，
∵x+y+z=2，
∴
+
+
≤
=2
，
∴
+
+
的最大值是2
．
故选：C．
∴（1+2+3）（x+y+z）≥（
| x |
| 2y |
| 3z |
∵x+y+z=2，
∴
| x |
| 2y |
| 3z |
| 6•2 |
| 3 |
∴
| x |
| 2y |
| 3z |
| 3 |
故选：C．
点评：本题考查三元柯西不等式及应用，考查基本的运算能力，是一道基础题．
练习册系列答案
相关题目
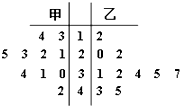从甲、乙两个城市分别随机抽取10台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示）．设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点M（x，y）与两定点O（0，0），A（3，0）的距离之比为
，那么满足条件的点M（x，y）所构成的曲线方程为（ ）
| 1 |
| 2 |
| A、圆（x+1）2+y2=2 |
| B、圆（x-1）2+y2=2 |
| C、圆（x+1）2+y2=4 |
| D、圆（x+2）2+y2=2 |
半径为3，中心角为120°的扇形面积为（ ）
| A、4π2 |
| B、3π |
| C、6π |
| D、2π2 |
已知函数f（x）=x2+alnx，若对任意两个不等的正数x1，x2（x1＞x2），都有f（x1）-f（x2）＞2（x1-x2）成立，则实数a的取值范围是（ ）
A、a＞
| ||
B、a≥
| ||
| C、a＞0 | ||
| D、a＞2 |
若a＞b＞0则下列不等式不成立的是（ ）
A、
| ||||
| B、|a|＞|b| | ||||
C、log
| ||||
D、a+b＜2
|
同时掷两个骰子，“向上的点数之和大于8”的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|