题目内容
9.已知双曲线C与椭圆$\frac{{x}^{2}}{27}+\frac{{y}^{2}}{36}=1$有相同的焦点,且经过点($\sqrt{15}$,4).(1)求双曲线的标准方程;
(2)若F1,F2为双曲线的两个焦点,点P在双曲线上,且∠F1PF2=120°.求△PF2F1的面积.
分析 (1)根据已知中双曲线与椭圆$\frac{{x}^{2}}{27}+\frac{{y}^{2}}{36}=1$有相同焦点,我们可以设出双曲线的标准方程(含参数a),然后根据经过点($\sqrt{15}$,4),得到一个关于a的方程,解方程,即可得到a2的值,进而得到双曲线的方程.
(2)由题意可得F1 (0,-3),F2(0,3),由余弦定理可得|PF1|•|PF2|=$\frac{20}{3}$,由S=$\frac{1}{2}$|PF1|•|PF2|sin120°,求得△F1PF2的面积.
解答 解:(1)椭圆$\frac{{x}^{2}}{27}+\frac{{y}^{2}}{36}=1$的焦点为(0,±3),c=3,
设双曲线方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{9-{a}^{2}}$=1,
∵过点($\sqrt{15}$,4),则$\frac{16}{{a}^{2}}$-$\frac{15}{9-{a}^{2}}$=1
得a2=4或36,而a2<9,∴a2=4,
双曲线方程为$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{5}$=1;
(2)由题意可得,a=2,b=$\sqrt{5}$,c=3,得F1 (0,-3),F2(0,3),
又|F1F2|2=36,||PF1|-|PF2||=4,
由余弦定理可得:
|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos120°=(|PF1|-|PF2|)2+3|PF1|•|PF2|=16+3|PF1|•|PF2|=36,
∴|PF1|•|PF2|=$\frac{20}{3}$
∴△F1PF2的面积S=$\frac{1}{2}$|PF1|•|PF2|sin120°=$\frac{1}{2}×\frac{20}{3}×\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{3}$.
点评 本题考查的知识点是双曲线的标准方程,余弦定理,以及双曲线的简单性质的应用,根据已知条件设出双曲线的标准方程(含参数a),并构造一个关于a的方程,是解答本题的关键.

| A. | 7 | B. | 15 | C. | 35 | D. | 21 |
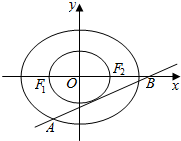 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).