题目内容
19．解不等式：|3x+2|+|2x-4|≥10．分析 直接运用零点分段法解不等式，其零点分别为x=-$\frac{8}{5}$或x=$\frac{12}{5}$，分三段讨论，再综合．
解答 解：运用零点分段法求解，过程如下：
①当x≥2时，3x+2+2x-4≥10，
即5x-12≥0，解得，x≥$\frac{12}{5}$，
②当-$\frac{2}{3}$≤x＜2时，3x+2-2x+4≥10，
即x-4≥0，无解，
③当x＜-$\frac{2}{3}$时，-3x-2-2x+4≥10，
即5x+8≤0，解得，x≤-$\frac{8}{5}$，
综合以上讨论得，x≥$\frac{12}{5}$或x≤-$\frac{8}{5}$，
即原不等式的解集为：（-∞，-$\frac{8}{5}$]∪[$\frac{12}{5}$，+∞）．
点评 本题主要考查了绝对值不等式的解法，涉及零点分段法的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
14．直线y=x+1与椭圆4x2+y2=λ（λ≠0）只有一个公共点，则λ等于（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{5}{4}$ | C． | $\frac{5}{3}$ | D． | $\frac{3}{5}$ |
4．
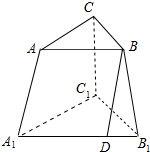在三棱台A1B1C1-ABC中，点D在A1B1上，且AA1∥BD，点M是△A1B1C1内（含边界）的一个动点，且有平面BDM∥平面A1C，则动点M的轨迹是（ ）
在三棱台A1B1C1-ABC中，点D在A1B1上，且AA1∥BD，点M是△A1B1C1内（含边界）的一个动点，且有平面BDM∥平面A1C，则动点M的轨迹是（ ）| A． | 平面 | B． | 直线 | ||
| C． | 线段，但只含1个端点 | D． | 圆 |