题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x(-2≤x<0)}\\{{x}^{\frac{1}{2}}(0≤x≤9)}\end{array}\right.$,若方程f(x)-a=0有两个解,则a的取值范围是(-$\frac{1}{4}$,2].分析 画出f(x)的图象,由二次函数及幂函数的性质求得f(x)的取值范围,即可求得a的取值范围.
解答  解:由-2≤x<0,f(x)=x2+x,对称轴x=-$\frac{1}{2}$,
解:由-2≤x<0,f(x)=x2+x,对称轴x=-$\frac{1}{2}$,
则-2≤x<-$\frac{1}{2}$时,f(x)单调递减,-$\frac{1}{2}$<x<0,f(x)单调递增,
当x=-2时,取最大值,最大值为2,当x=-$\frac{1}{2}$时取最小值,最小值为-$\frac{1}{4}$,
当0≤x≤9时,f(x)=${x}^{\frac{1}{2}}$,f(x)在[0,9]上单调递增,
若方程f(x)-a=0有两个解,则f(x)=a与f(x)有两个交点,
则a的取值范围(-$\frac{1}{4}$,2],
∴a的取值范围(-$\frac{1}{4}$,2],
故答案为:(-$\frac{1}{4}$,2].
点评 本题考查二次函数的及幂函数图象与性质,考查分段函数的单调性,考查数形结合思想,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
8.已知集合A={x|y=lgx},B={x|x-1≤0},则A∩B=( )
| A. | (0,1] | B. | (0,1) | C. | (-1,1] | D. | [1,+∞) |
9.将周期为π的函数f(x)=2sin(ωx+$\frac{π}{3}$),(ω>0)的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最小正值是( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.已知D,E是△ABC边BC的三等分点,点P在线段DE上,若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则xy的取值范围是( )
| A. | [$\frac{1}{9}$,$\frac{4}{9}$] | B. | [$\frac{1}{9}$,$\frac{1}{4}$] | C. | [$\frac{2}{9}$,$\frac{1}{2}$] | D. | [$\frac{2}{9}$,$\frac{1}{4}$] |
18.下表是某校高三一次月考5个班级的数学、物理的平均成绩:
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程$\hat y=\hat bx+\hat a$;
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| 班级 | 1 | 2 | 3 | 4 | 5 |
| 数学(x分) | 111 | 113 | 119 | 125 | 127 |
| 物理(y分) | 92 | 93 | 96 | 99 | 100 |
(Ⅱ)从以上5个班级中任选两个参加某项活动,求至少有一个班级数学平均分在115分以上的概率.
附:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
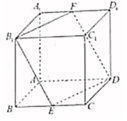 在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.