题目内容
已知正数x、y满足xy=x+y+3.
(1)求xy的范围;
(2)求x+y的范围.
(1)求xy的范围;
(2)求x+y的范围.
考点:基本不等式在最值问题中的应用
专题:不等式的解法及应用
分析:(1)根据x+y≥2
,将xy=x+y+3中的x+y消去,然后解不等式可求出xy的范围,注意等号成立的条件;
(2)根据xy≤(
)2,将xy=x+y+3中的xy消去,然后解不等式可求出x+y的范围,注意等号成立的条件.
| xy |
(2)根据xy≤(
| x+y |
| 2 |
解答:
解:(1)∵正数x、y满足x+y+3=xy,
∴xy=x+y+3≥3+2
,即xy-2
-3≥0,可以变形为(
-3)(
+1)≥0,
∴
≥3,即xy≥9,
当且仅当x=y=3时取等号,
∴xy的范围是[9,+∞);
(2)∵x、y均为正数,
∴x+y≥2
,则xy≤(
)2,
∴x+y+3=xy≤(
)2,即(x+y)2-4(x+y)-12≥0,
化简可得,(x+y+2)(x+y-6)≥0,
∴x+y≥6,
当且仅当x=y=3时取等号,
∴x+y的范围是[6,+∞).
∴xy=x+y+3≥3+2
| xy |
| xy |
| xy |
| xy |
∴
| xy |
当且仅当x=y=3时取等号,
∴xy的范围是[9,+∞);
(2)∵x、y均为正数,
∴x+y≥2
| xy |
| x+y |
| 2 |
∴x+y+3=xy≤(
| x+y |
| 2 |
化简可得,(x+y+2)(x+y-6)≥0,
∴x+y≥6,
当且仅当x=y=3时取等号,
∴x+y的范围是[6,+∞).
点评:本题考查了基本不等式在最值问题中的应用.在应用基本不等式求最值时要注意“一正、二定、三相等”的判断.运用基本不等式解题的关键是寻找和为定值或者是积为定值,难点在于如何合理正确的构造出定值.属于中档题.

练习册系列答案
相关题目
 如图,是一个算法程序框图,在集合A={x|-10≤x≤10,x∈R}中随机抽取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率为( )
如图,是一个算法程序框图,在集合A={x|-10≤x≤10,x∈R}中随机抽取一个数值做为x输入,则输出的y值落在区间(-5,3)内的概率为( )| A、0.4 | B、0.5 |
| C、0.6 | D、0.8 |
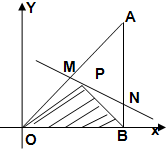 如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P
如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P