题目内容
已知抛物线y2=4x上两个动点B,C和点A(1,2),且∠BAC=90°.求证:动直线BC必过定点.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出抛物线上的点B(
,a),C(
,b),由∠BAC=90°借助于向量数量积等于0得到a,b的关系,由两点式求出BC所在直线的斜率,写出BC的点斜式方程,与a,b的关系式结合后由直线系方程得答案.
| a2 |
| 4 |
| b2 |
| 4 |
解答:
证明:设B(
,a),C(
,b),而A(1,2),
∴
=(
-1,a-2),
=(
-1,b-2),
由于∠BAC=90°,得向量
⊥
,
•
=0.
即(
-1,a-2)•(
-1,b-2)=0.
整理得ab+2a+2b+20=0.
而过BC的直线的斜率为:
=
.
∴过BC的直线方程为y-b=
(x-
),
整理得4x+ab-(a+b)y=0,即4x-(a+b)y-2a-2b-20=0.
化为4x-20-(a+b)(y+2)=0.可得直线恒过定点(5,-2).
∴直线必过定点(5,-2)
| a2 |
| 4 |
| b2 |
| 4 |
∴
| AB |
| a2 |
| 4 |
| AC |
| b2 |
| 4 |
由于∠BAC=90°,得向量
| AB |
| AC |
| AB |
| AC |
即(
| a2 |
| 4 |
| b2 |
| 4 |
整理得ab+2a+2b+20=0.
而过BC的直线的斜率为:
| a-b | ||||
|
| 4 |
| a+b |
∴过BC的直线方程为y-b=
| 4 |
| a+b |
| b2 |
| 4 |
整理得4x+ab-(a+b)y=0,即4x-(a+b)y-2a-2b-20=0.
化为4x-20-(a+b)(y+2)=0.可得直线恒过定点(5,-2).
∴直线必过定点(5,-2)
点评:本题考查了抛物线的简单几何性质,考查了直线系方程的运用,是中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
已知函数f(x)在R上满足f(1+x)=2f(1-x)-x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、3x-y-2=0 |
| B、3x+y-2=0 |
| C、x-y+1=0 |
| D、x-y-2=0 |
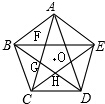 如图,求边长为1的正五边形的对角线围成的正五边形的边长.
如图,求边长为1的正五边形的对角线围成的正五边形的边长.