题目内容
设x，y满足
，则z=x+y的最小值为（ ）
|
| A、-8 | B、-7 | C、-6 | D、-5 |
考点：简单线性规划
专题：不等式的解法及应用
分析：先画出约束条件
的可行域，再求出可行域中各角点的坐标，将各点坐标代入目标函数的解析式，分析后易得目标函数x+y的最小值．
|
解答：
解：由约束条件
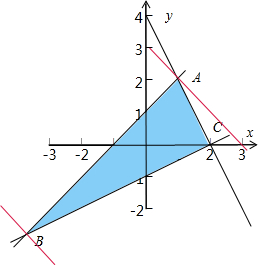
得如图所示的三角形区域，
令x+y=z，y=-x+z，
显然当平行直线过点B时，z取得最小值；由
，可得B（-3，-4），
此时z=-7．
故选：B．
解：由约束条件
|
令x+y=z，y=-x+z，
显然当平行直线过点B时，z取得最小值；由
|
此时z=-7．
故选：B．
点评：在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．
练习册系列答案
相关题目
函数f（x）=log
（x2+3x-4）的单调递增区间为（ ）
| 1 |
| 2 |
| A、（0，+∞） |
| B、（-∞，0） |
| C、（1，+∞） |
| D、（-∞，-4） |
若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下面命题正确的是（ ）
| A、若m?β，α⊥β，则m⊥α |
| B、若α∩γ=m，β∩γ=n，则α∥β |
| C、若m⊥β，m∥α，则α⊥β |
| D、若α⊥β，α⊥γ，则β⊥γ |
从只含有二件次品的10个产品中取出三件，设A为“三件产品全不是次品”，B为“三件产品全是次品”，C 为“三件产品不全是次品”，则下列结论正确的是（ ）
| A、事件A与C互斥 |
| B、事件C是随机事件 |
| C、任两个均互斥 |
| D、事件B是不可能事件 |
函数f（x）=1-xlnx的零点所在区间是（ ）
A、（0，
| ||
B、（
| ||
| C、（1，2） | ||
| D、（2，3） |
从20名高一学生、20名高二学生和10名高三学生且有艺术特长的学生中，选1人参加元旦文艺演出，共有选法种数为（ ）
| A、50 | B、10 | C、60 | D、500 |
在△ABC中，sinAsinC＞cosAcosC，则△ABC一定是（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不确定 |
在等差数列{an}中，a1=15，d=-2，则a9=（ ）
| A、-1 | B、1 | C、2 | D、-3 |