题目内容
椭圆
+
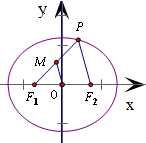
=1上一点P到左焦点F1的距离为2,M是线段PF1的中点,则M到原点O的距离等于( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、2 | B、6 | C、4 | D、8 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆的定义,得|PF1|+|PF2|=2a,可得|PF2|=2a-|PF1|=8,在△PF1F2中利用中位线定理,即可得到的|OM|值.
解答:
 解:∵椭圆
解:∵椭圆
+
=1中,a=5,
∴|PF1|+|PF2|=2a=10,
结合|PF1|=2,得|PF2|=2a-|PF1|=10-2=8,
∵OM是△PF1F2的中位线,
∴|OM|=
|PF2|=
×8=4.
故选:C.
 解:∵椭圆
解:∵椭圆| x2 |
| 25 |
| y2 |
| 9 |
∴|PF1|+|PF2|=2a=10,
结合|PF1|=2,得|PF2|=2a-|PF1|=10-2=8,
∵OM是△PF1F2的中位线,
∴|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
故选:C.
点评:本题给出椭圆的焦点三角形的一边长,求另一边中点到原点的距离,着重考查了椭圆的定义和标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
已知i为虚数单位,复数z=
,则复数z的共轭复数的虚部为( )
| i |
| -1+i |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
设x,y满足
,则z=x+y的最小值为( )
|
| A、-8 | B、-7 | C、-6 | D、-5 |
在极坐标系中,以点(
,
)为圆心,
为半径的圆的方程为( )
| a |
| 2 |
| π |
| 2 |
| a |
| 2 |
| A、ρ=acosθ |
| B、ρ=asinθ |
| C、ρcosθ=a |
| D、ρsinθ=a |
一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):
则第9行中的第4个数是( )
| 第一行 | 1 |
| 第二行 | 2、3 |
| 第三行 | 4、5、6、7 |
| … | … |
| A、132 | B、255 |
| C、259 | D、260 |
下列各组函数是同一函数的是( )
①f(x)=
与g(x)=x
;
②f(x)=|x|与g(x)=(
)2;
③f(x)=x0与g(x)=
;
④f(x)=x2-2x-1与g(t)=t2-2t-1.
①f(x)=
| -2x3 |
| -2x |
②f(x)=|x|与g(x)=(
| x |
③f(x)=x0与g(x)=
| 1 |
| x0 |
④f(x)=x2-2x-1与g(t)=t2-2t-1.
| A、①② | B、①③ | C、③④ | D、①④ |
若偶函数f(x)在[-1,0]上为减函数,α,β为任意一锐角三角形的两个内角,则( )
| A、f(cosα)>f(cosβ) |
| B、f(sinα)>f(sinβ) |
| C、f(sinα)>f(cosβ) |
| D、f(cosα)>f(sinβ) |
在△ABC中,已知a=6,b=8,C=45°,则△ABC的面积为( )
A、24
| ||
B、12
| ||
C、6
| ||
D、8
|