题目内容
设点M为抛物线y2=2px(p>0)上一动点,F为焦点,O为坐标原点,求
的取值范围.
| |MO| |
| |MF| |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:由抛物线方程为:y2=2px(p>0),可得:焦点F的坐标,由抛物线的定义可得
=
,化简再换元,利用基本不等式求得最大值.
| |MO| |
| |MF| |
| |MO| |
| d |
解答:
解:由抛物线方程为:y2=2px(p>0),可得:
焦点F(
,0),
设M(m,n),则n2=2pm,m>0,设M 到准线x=-
的距离等于d,
则
=
=
=
=
=
.
令 pm-
=t,t>-
,则 m=
+
,
∴
=
=
≤
=
(当且仅当 t=
时,等号成立).
故
的最大值为
,
的取值范围(0,
].
焦点F(
| p |
| 2 |
设M(m,n),则n2=2pm,m>0,设M 到准线x=-
| p |
| 2 |
则
| |MO| |
| |MF| |
| |MO| |
| d |
| ||
m+
|
| ||
m+
|
|
1+
|
令 pm-
| p2 |
| 4 |
| p2 |
| 4 |
| t |
| p |
| p |
| 4 |
∴
| |MO| |
| |MF| |
1+
|
1+
|
1+
|
2
| ||
| 3 |
| 3p2 |
| 4 |
故
| |MO| |
| |MF| |
2
| ||
| 3 |
| |MO| |
| |MF| |
2
| ||
| 3 |
点评:本题考查抛物线的定义、基本不等式的应用,考查换元的思想,解题的关键是表达出
,再利用基本不等式,综合性强.
| |MO| |
| |MF| |

练习册系列答案
相关题目
函数y=x2-x+2在下列哪个区间上是单调减函数( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
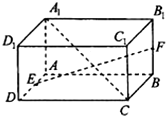 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.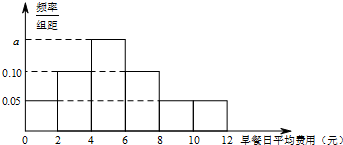 某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.
某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.