题目内容
7．复数z=$\frac{-3-i}{2-i}$在复平面内对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据复数的运算法则，化简复数z即可得出结论．
解答 解：∵复数$z=\frac{-3-i}{2-i}$=$\frac{（-3-i）（2+i）}{（2-i）（2+i）}$=$\frac{-5-5i}{5}$=-1-i，
∴z在复平面内对应的点位于第三象限．
故选：C．
点评 本题考查了复数的化简与运算问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．已知函数f（x）=$\left\{{\begin{array}{l}{3+{{log}_2}x，x＞0}\\{{x^2}-x-1，x≤0}\end{array}}$，则不等式f（x）≤5的解集为（ ）
| A． | [-1，1] | B． | （-∞，-2]∪（0，4） | C． | [-2，4] | D． | （-∞，-2]∪[0，4] |
2．设定义在区间（0，$\frac{π}{2}$）上的函数y=sin2x的图象与y=$\frac{1}{2}$cosx图象的交点横坐标为α，则tanα的值为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | $\frac{\sqrt{15}}{15}$ | D． | 1 |
19．对于椭圆${C_{（a，b）}}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a，b＞0，a≠b）$．若点（x0，y0）满足$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}＜1$．则称该点在椭圆C（a，b）内，在平面直角坐标系中，若点A在过点（2，1）的任意椭圆C（a，b）内或椭圆C（a，b）上，则满足条件的点A构成的图形为（ ）
| A． | 三角形及其内部 | B． | 矩形及其内部 | C． | 圆及其内部 | D． | 椭圆及其内部 |
16．如图，已知三棱锥P-ABC的底面是等腰直角三角形，且∠ACB=90°，侧面PAB⊥底面ABC，AB=PA=PB=4．则这个三棱锥的三视图中标注的尺寸x，y，z分别是（ ）
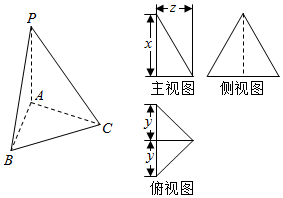
| A． | $2\sqrt{3}$，$2\sqrt{2}$，2 | B． | 4，2，$2\sqrt{2}$ | C． | $2\sqrt{3}$，2，2 | D． | $2\sqrt{3}$，2，$2\sqrt{2}$ |