题目内容
16.如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=90°,侧面PAB⊥底面ABC,AB=PA=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )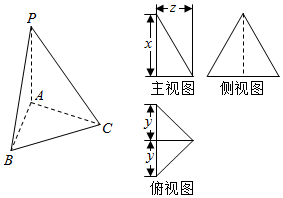
| A. | $2\sqrt{3}$,$2\sqrt{2}$,2 | B. | 4,2,$2\sqrt{2}$ | C. | $2\sqrt{3}$,2,2 | D. | $2\sqrt{3}$,2,$2\sqrt{2}$ |
分析 根据题意,结合三视图的特征,得出x是等边△PAB边AB上的高,y是边AB的一半,z是等腰直角△ABC斜边AB上的中线,分别求出它们的大小即可.
解答 解:∵三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=90°,
侧面PAB⊥底面ABC,AB=PA=PB=4;
∴x是等边△PAB边AB上的高,x=4sin60°=2$\sqrt{3}$,
y是边AB的一半,y=$\frac{1}{2}$AB=2,
z是等腰直角△ABC斜边AB上的中线,z=$\frac{1}{2}$AB=2;
∴x,y,z分别是2$\sqrt{3}$,2,2.
故选:C.
点评 本题考查了几何体的三视图与直观图的关系与应用问题,也考查了计算能力与空间想象能力,是基础题.

练习册系列答案
相关题目
7.复数z=$\frac{-3-i}{2-i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.已知数列{an}为等差数列,a1+a8+a15=π,则cos(a4+a12)则的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $±\frac{\sqrt{3}}{2}$ |
1.函数f(x)=loga(6-ax)在(0,2)上为减函数,则a的取值范围是( )
| A. | (1,3] | B. | (1,3) | C. | (0,1) | D. | [3,+∞) |
5.若全集U={1,2,3,4,5,6},M={1,4,5},N={2,3},则集合(∁UN)∩M=( )
| A. | {2,3} | B. | {2,3,5} | C. | {1,4} | D. | {1,4,5} |