��Ŀ����
19��������Բ${C_{��a��b��}}��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��a��b��$�����㣨x0��y0������$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}��1$����Ƹõ�����ԲC��a��b���ڣ���ƽ��ֱ������ϵ�У�����A�ڹ��㣨2��1����������ԲC��a��b���ڻ���ԲC��a��b���ϣ������������ĵ�A���ɵ�ͼ��Ϊ��������| A�� | �����μ����ڲ� | B�� | ���μ����ڲ� | C�� | Բ�����ڲ� | D�� | ��Բ�����ڲ� |
���� ��A��x0��y0���ڹ���P��2��1����������ԲC��a��b���ڻ���ԲC��a��b���ϣ��ɵ�$\frac{4}{{a}^{2}}+\frac{1}{{b}^{2}}$=1��$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$��1������Բ�ĶԳ��Կ�֪����B��-2��1������C��-2��-1������D��2��-1��������������Բ�ϣ����ɵó���
��� �⣺���A��x0��y0���ڹ���P��2��1����������ԲC��a��b���ڻ���ԲC��a��b���ϣ�
��$\frac{4}{{a}^{2}}+\frac{1}{{b}^{2}}$=1��$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$��1��
��$\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$��$\frac{4}{{a}^{2}}+\frac{1}{{b}^{2}}$=1��
����Բ�ĶԳ��Կ�֪����B��-2��1������C��-2��-1������D��2��-1��������������Բ�ϣ�
��֪�����������ĵ�A���ɵ�ͼ��Ϊ����PBCD�����ڲ���
��ѡ��B��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⣬���������ν�Ϸ�����������������������������е��⣮

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�| A�� | 3 | B�� | 0 | C�� | -3 | D�� | $\frac{1}{3}$ |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
| ���ʽ | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
| Ƶ�� | 35 | 25 | a | 10 | b |
������a��b��ֵ��
���������ֻ���3���˿��У�ÿ�˽�����һ���ֻ�����ǡ����1���˿ͷ�4�ڸ���ĸ��ʣ�
������ר��������һ��ƻ��6S�ֻ����˿ͷ�1�ڸ����ȫ���������Ϊ1000Ԫ����2�ڻ�3�ڸ��������Ϊ1500Ԫ����4�ڻ�5�ڸ��������Ϊ2000Ԫ����X��ʾ����һ��ƻ��6S�ֻ���������X�ķֲ��м���ѧ������
| A�� | -$\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\frac{1}{2}$ | D�� | $��\frac{\sqrt{3}}{2}$ |
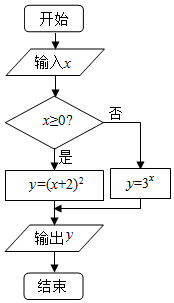
 ִ����ͼ��ʾ�ij����ͼ�������SֵΪ��������
ִ����ͼ��ʾ�ij����ͼ�������SֵΪ��������| A�� | 42 | B�� | 19 | C�� | 8 | D�� | 3 |