题目内容
用一个平面去截一个几何体，得到的截面是圆面，这个几何体不可能是（ ）
| A、棱锥 | B、圆柱 | C、球 | D、圆锥 |
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：从几何体分截面图形判断即可．
解答：
解：用一个平面去截一个棱锥，得到的截面是三角形，不可能是圆，所以A正确；
用一个平面去截一个圆柱，截面与底面平行，得到的截面是圆面，所以B不满足题目要求；
用一个平面去截一个球，得到的截面是圆面，所以C不满足题目要求；
用一个平面去截一个圆锥，截面与底面平行，得到的截面是圆面，所以D不满足题目要求；
故选：A．
用一个平面去截一个圆柱，截面与底面平行，得到的截面是圆面，所以B不满足题目要求；
用一个平面去截一个球，得到的截面是圆面，所以C不满足题目要求；
用一个平面去截一个圆锥，截面与底面平行，得到的截面是圆面，所以D不满足题目要求；
故选：A．
点评：本题考查空间几何体的特征，考查空间想象能力．
练习册系列答案
名校课堂系列答案
相关题目
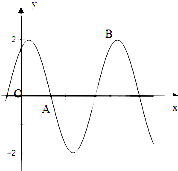函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，图象与x轴交点A及图象最高点B的坐标分别是A（| π |
| 3 |
| 13π |
| 12 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
| D、命题“?x∈R使得x2+x+1＜0”的否定是“?x∈R均有x2+x+1＜0” |
△ABC内角A，B，C的对边分别为a，b，c．已知a=3，A=60°，b=
，则B=（ ）
| 6 |
| A、45° | B、30° |
| C、60° | D、135° |