题目内容
12.若曲线y=x3,在点P处的切线方程为y=3x-2,则点P的坐标为( )| A. | (2,4) | B. | (-1,-1) | C. | (1,1)或(-1,-1) | D. | (1,1) |
分析 设出P的坐标,表示出切线方程,从而求出P的坐标即可.
解答 解:设P(a,a3),
则y′=3x2,y′|x=a=3a2,
故切线方程是:y-a3=3a2(x-a),
即y=3a2x-2a3,由y=3x-2,得:a=1,
故P(1,1),
故选:D.
点评 本题考查了切线方程问题,考查导数的应用,是一道基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
2.已知函数$f(x)=lnx-x+\frac{1}{x}$,若a=f(3),b=f(π),c=f(5),则( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<c<b |
3.a,b为正实数,若函数f(x)=ax3+bx+ab-1是奇函数,则f(2)的最小值是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
7.已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f($\frac{6}{5}$),b=f($\frac{3}{2}$),c=f($\frac{1}{2}$),则( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
4.下列结论正确的是( )
| A. | 两个面平行,其余各面都是平行四边形所围成的几何体一定是棱柱 | |
| B. | 若△ABC中,$\overrightarrow{AB}$•$\overrightarrow{BC}$<0,则△ABC是钝角三角形 | |
| C. | 函数f(x)=x+$\frac{4}{x-1}$(x>1)的最小值为5 | |
| D. | 若G2=ab,则G是a,b的等比中项 |
2.若直线y=-2mx-6与直线y=(m-3)x+7平行,则m的值为( )
| A. | -1 | B. | 1或-1 | C. | 1 | D. | 3 |
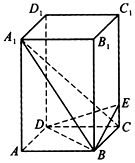 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1