题目内容
15．若a＞b＞0，且ab=1，则下列不等式成立的是（ ）| A． | a+$\frac{1}{b}$＜$\frac{b}{{2}^{a}}$＜log2（a+b）） | B． | $\frac{b}{{2}^{a}}$＜log2（a+b）＜a+$\frac{1}{b}$ | ||
| C． | a+$\frac{1}{b}$＜log2（a+b）＜$\frac{b}{{2}^{a}}$ | D． | log2（a+b））＜a+$\frac{1}{b}$＜$\frac{b}{{2}^{a}}$ |
分析 a＞b＞0，且ab=1，可取a=2，b=$\frac{1}{2}$．代入计算即可得出大小关系．
解答 解：∵a＞b＞0，且ab=1，
∴可取a=2，b=$\frac{1}{2}$．
则$a+\frac{1}{b}$=4，$\frac{b}{{2}^{a}}$=$\frac{\frac{1}{2}}{{2}^{2}}$=$\frac{1}{8}$，log2（a+b）=$lo{g}_{2}（2+\frac{1}{2}）$=$lo{g}_{2}\frac{5}{2}$∈（1，2），
∴$\frac{b}{{2}^{a}}$＜log2（a+b）＜a+$\frac{1}{b}$．
故选：B．
点评 本题考查了函数的单调性、不等式的解法与性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
10．已知a∈R，i是虚数单位，若z=a+$\sqrt{3}$i，z•$\overline{z}$=4，则a=（ ）
| A． | 1或-1 | B． | $\sqrt{7}$或-$\sqrt{7}$ | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |
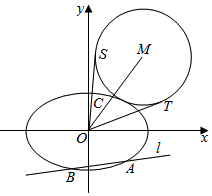在平面直角坐标系xOy中，椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，焦距为2．