题目内容
18．
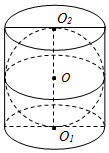如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$．
分析 设出球的半径，求出圆柱的体积以及球的体积即可得到结果．
解答 解：设球的半径为R，则球的体积为：$\frac{4}{3}π$R3，
圆柱的体积为：πR2•2R=2πR3．
则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{2π{R}^{3}}{\frac{4π{R}^{3}}{3}}$=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．
点评 本题考查球的体积以及圆柱的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
10．已知a∈R，i是虚数单位，若z=a+$\sqrt{3}$i，z•$\overline{z}$=4，则a=（ ）
| A． | 1或-1 | B． | $\sqrt{7}$或-$\sqrt{7}$ | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |
在平面直角坐标系xOy中，椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，焦距为2．