如图.圆O的半径OA与OB相互垂直.E为圆O上一点.直线OB与圆O交于另一点F.与直线AE交于点D.过点E的切线CE交线段于点C.求证:CD2=CB•CF．题目和参考答案——青夏教育精英家教网——

题目内容

18．

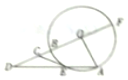如图，圆O的半径OA与OB相互垂直，E为圆O上一点，直线OB与圆O交于另一点F，与直线AE交于点D，过点E的切线CE交线段于点C，求证：CD²=CB•CF．

分析连接OE，则OE⊥CE，证明CD=CE，利用CE是圆O的切线，可得CE²=CB•CF，即可证明结论．

解答证明：连接OE，则OE⊥CE，
∵OE=OA，∴∠OEA=∠OAE，
∵OA⊥OB，∴∠ODA+∠OAE=90°，
∵OE⊥CE，∴∠OEA+∠CED=90°，
∴∠ODA=∠CED，
∴CD=CE，
∵CE是圆O的切线，
∴CE²=CB•CF，
∴CD²=CB•CF．

点评本题考查圆的切线的性质，考查学生分析解决问题的能力，属于中档题．

练习册系列答案

教学练新同步练习系列答案

黄冈小状元作业本系列答案

课时达标练与测系列答案

课前课后同步练习系列答案

经纶学典课时作业系列答案

课堂小作业系列答案

黄冈小状元口算速算练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

浙江名卷系列答案

相关题目

8．设a为实数，函数f（x）=e^x-x+a，x∈R．
（1）求f（x）在区间[-1，2]上的最值；
（2）求证：当a＞-1，且x＞0时，${e^x}＞\frac{1}{2}{x^2}-ax+1$．

9．2016年某市为了促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计60吨厨余垃圾，假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱的投放量分别为x，y，z，其中x＞0，x+y+z=60，则数据x，y，z的标准差的最大值为20$\sqrt{2}$．
（注：方差${s^2}=\frac{1}{n}[{{{（{{x_1}-\overline x}）}^2}+{{（{{x_2}-\overline x}）}^2}+…+{{（{{x_n}-\overline x}）}^2}}]$，其中$\overline x$为x₁，x₂，…，x_n的平均数）

6．分别从集合M{1，2，3}和集合N={4，5，6}中各取一个数，则这两个数之和为偶数的概率为$\frac{4}{9}$．

13．若实数x，y满足x²+y²-2y=0，且（k-1）x-y-3k+5≤0恒成立，则实数k的取值范围为k≥$\frac{7}{4}$．

3．若复数z满足（1+i）z=2-i，则复数z在复平面内对应的点在（　　）

10．二项式${（\frac{1}{2}\sqrt{x}+\frac{2}{\root{3}{x}}）}^{6}$的展开式中第四项的系数为20．

某程序框图如图所示，若运行该程序后输出S为$\frac{5}{6}$．

8．在直角坐标系xOy中，曲线${C_1}：\left\{\begin{array}{l}x=1+2t\\ y=2-2t\end{array}\right.$（t为参数，t∈R），曲线${C_2}：\left\{\begin{array}{l}x=2cosθ+2\\ y=2sinθ\end{array}\right.$（θ为参数，θ∈[0，2π]）．
（Ⅰ）以O为极点，x轴正半轴为极轴，取相同的长度单位建立极坐标系，求曲线C₂的极坐标方程；
（Ⅱ）若曲线C₁与曲线C₂相交于点A、B，求|AB|．