题目内容
如图,已知几何体的三视图(单位:cm).
(1)在这个几何体的直观图相应的位置标出字母A,B,C,D,A1,B1,C1,D1,P,Q;
(2)求这个几何体的表面积及体积;
(3)设异面直线A1Q、PD所成角为θ,求cosθ.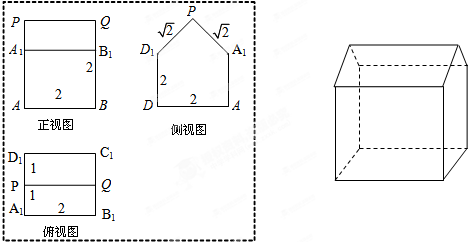
(1)在这个几何体的直观图相应的位置标出字母A,B,C,D,A1,B1,C1,D1,P,Q;
(2)求这个几何体的表面积及体积;
(3)设异面直线A1Q、PD所成角为θ,求cosθ.

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:(1)根据三视图的画出,进行复原画出几何体的图形即可.
(2)几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体,求出底面面积,然后求出体积即可.
(3)由PQ∥CD,且PQ=CD,可得:PD∥QC,故∠A1QC即为异面直线A1Q、PD所成角(或其补角),利用余弦定理和勾股定理解三角形可得答案.
(2)几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体,求出底面面积,然后求出体积即可.
(3)由PQ∥CD,且PQ=CD,可得:PD∥QC,故∠A1QC即为异面直线A1Q、PD所成角(或其补角),利用余弦定理和勾股定理解三角形可得答案.
解答:
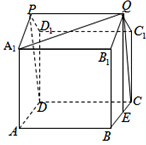
解:(1)这个几何体的直观图如图所示.

(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.
由PA1=PD1=
,A1D1=AD=2,
可得PA1⊥PD1.
故所求几何体的表面积
S=5×22+2×
2×1+2×
×2
=22+4
(cm2),
所求几何体的体积V=23+
×(
)2×2=10(cm3).
(3)由PQ∥CD,且PQ=CD,可得:PD∥QC,
故∠A1QC即为异面直线A1Q、PD所成角(或其补角),
由题意知:A1Q2=A1B12+B1Q2=6,A1C=
×2=2
.
取BC的中点E,则QE⊥BC,且QE=3,QC2=QE2+EC2=10,
由余弦定理得:cosθ=|cos∠A1QC|=|
|=
=
,
所以异面直线A1Q、PD所成角为θ满足cosθ=
.

(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体.
由PA1=PD1=
| 2 |
可得PA1⊥PD1.
故所求几何体的表面积
S=5×22+2×
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
所求几何体的体积V=23+
| 1 |
| 2 |
| 2 |
(3)由PQ∥CD,且PQ=CD,可得:PD∥QC,
故∠A1QC即为异面直线A1Q、PD所成角(或其补角),

由题意知:A1Q2=A1B12+B1Q2=6,A1C=
| 3 |
| 3 |
取BC的中点E,则QE⊥BC,且QE=3,QC2=QE2+EC2=10,
由余弦定理得:cosθ=|cos∠A1QC|=|
| A1Q2+QC2-A1C2 |
| 2A1Q•QC |
| 6+10-12 | ||||
2
|
| ||
| 15 |
所以异面直线A1Q、PD所成角为θ满足cosθ=
| ||
| 15 |
点评:本题考查三视图复原几何体,空间直线的夹角,画出中逐步按照三视图的作法复原,考查空间想象能力,逻辑推理能力,计算能力,转化思想,是中档题.

练习册系列答案
相关题目
把函数y=cos2x+3的图象沿向量
平移后得到函数y=sin(2x-
)的图象,则向量
是( )
| a |
| π |
| 6 |
| a |
A、(
| ||
B、(
| ||
C、(
| ||
D、(-
|
下列向量中与
=(2,3)垂直的是( )
| a |
| A、b=(-2,3) |
| B、c=(2,-3) |
| C、d=(3,-2) |
| D、e=(-3,-2) |
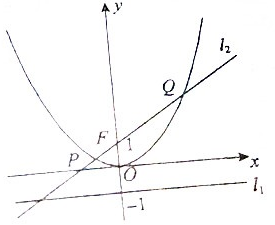 已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.
已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.