题目内容

已知△ABO三个顶点坐标为A（1，0），B（0，2），O（0，0），P（x，y）是坐标平面内一点，且满足
AP
•
OA
≤0，
BP
•
OB
≥0，则
OP
•
AB
的最小值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：首先，根据所给点的坐标，写出
AP
=(x-1，y)，
OA
=（1，0），
BP
=（x，y-2），
OB
=（0，2），然后，根据所给向量的条件，得到相应的取值情况．
解答： 解：∵A（1，0），B（0，2），O（0，0），P（x，y），
∴
AP
=(x-1，y)，
OA
=（1，0），
BP
=（x，y-2），
OB
=（0，2），
∵
AP
•
OA
≤0，
BP
•
OB
≥0，
∴
x-1≤0
2(y-2)≥0
，
∴
x≤1
y≥2
，
∵
AB
=（-1，2），
∵
OP
•
AB
=-x+2y，
∴
OP
•
AB
=-x+2y的最小值为3，
故答案为：3．
点评：本题重点考查了数量积的坐标运算、运算律等知识，属于中档题．
练习册系列答案
相关题目
已知圆C的方程为x2+y2-2x+4y=0，直线l：2x-y+t=0．
（1）若直线l与圆C相切，求实数t的取值；
（2）若直线l与圆C相交于M，N两点，且|MN|=
15
，求实数t的取值．
已知双曲线C的两个焦点坐标为F1（0，-3），F2（0，3），且一个焦点到其中一条渐近线的距离为
3
2
2
，则双曲线C的离心率为
 
．
已知函数y=
2-x
2+x
+
2x-2
的定义域为M．
（1）求M；
（2）当x∈M时，求函数f（x）=log2x•log2（x2）+alog2x的最小值．
已知f1（x）=log4x，f2（x）=log6x，f3（x）=log9x，若f1（n）=f2（m）=f3（m+n），则
m
n
=
 
．
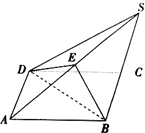如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面BDE⊥平面ABCD．
三个互不重合的平面，能把空间分成n个部分，则n所有可能值为
 
．
如图所示的抛物线y=-
1
20
（1+k2）x2+kx（k＞0，0≤x≤S）刻画的是某种炮弹发射后的飞行轨迹，其中x、y分别表示炮弹从发射点到即时位置在水平方向上和竖直方向上的位移，且其单位均为千米．炮弹的射程是指炮弹在地平面上的落地点的横坐标S，炮弹的射高是指炮弹飞行轨迹的最大高度．
（1）求当炮弹的射程为10千米时k值；
（2）求炮弹的射高关于k的函数g（k）；
（3）问：是否存在k的值，使得通过适当调整炮弹的发射方位，就能击中飞行高度为5千米的飞行物．
把函数y=cos2x+3的图象沿向量
a
平移后得到函数y=sin（2x-
π
6
）的图象，则向量
a
是（　　）
A、（
π
3
，-3）
B、（
π
6
，3）
C、（
π
12
，-3）
D、（-
π
12
，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网