题目内容
函数f(x)=
ax3+
bx2+x的单调增区间是(-1,
),则 ab= .
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由函数f(x)=
ax3+
bx2+x的单调增区间是(-1,
),得f′(x)=ax2+bx+1>0的解集是(-1,
),从而方程ax2+bx+1=0的两根是-1,
,
由一元二次方程根与系数的关系求出ab即可.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由一元二次方程根与系数的关系求出ab即可.
解答:
解:∵函数f(x)=
ax3+
bx2+x的单调增区间是(-1,
),
∴f′(x)=ax2+bx+1>0的解集是(-1,
),
∴方程ax2+bx+1=0的两根是-1,
,
∴-1+
=-
,-1×
=
,
∴a=-2,b=1,
∴ab=2.
故答案为:2.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f′(x)=ax2+bx+1>0的解集是(-1,
| 1 |
| 2 |
∴方程ax2+bx+1=0的两根是-1,
| 1 |
| 2 |
∴-1+
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| 1 |
| a |
∴a=-2,b=1,
∴ab=2.
故答案为:2.
点评:本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
相关题目

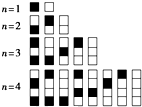 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示:由此推断,当n=8时,黑色正方形互不相邻的着色方案共有