题目内容
等差数列{an}中,a1+a2=2,a3+a4=4,则a7+a8的值为( )
| A、4 | B、6 | C、8 | D、10 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:本题已知第一个二项的和,第二个二项的和,求第四个二项的和,可以由数列的性质Sk,S2k-Sk,S3k-S2k,…是一个等差数列,计算出a7+a8的值.
解答:
解:∵在等差数列{an}中,Sk,S2k-Sk,S2k-Sk,…构成一个等差数列,a1+a2=2,a3+a4=4.
∴a1+a2,a3+a4,a5+a6,a7+a8,构成一个首项为2,公差为2的等差数列.
故a7+a8=2+2(4-1)=8,
故选:C.
∴a1+a2,a3+a4,a5+a6,a7+a8,构成一个首项为2,公差为2的等差数列.
故a7+a8=2+2(4-1)=8,
故选:C.
点评:本题考查等差数列的性质,正确解答本题关键是掌握了在等差数列{an}中,Sk,S2k-Sk,S2k-Sk,…构成一个等差数列这个性质,利用此性质求解本题信息论快捷.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
某厂去年的产值记为1,计划从今年起,每年的产值比上年增长8%,则从今年起到第十年,这个厂这十年的总产值为( )
| A、1.089 | ||
| B、1.0810 | ||
C、
| ||
D、
|
已知球O的表面积为16π,球心O在大小为
的二面角α-l-β的内部,且平面α与球O相切与点M,平面β截球O所得的小圆O′的半径为1(O′为小圆圆心),若点P为圆O上任意一点,记∠MOP为θ,则下列结论正确的是( )
| π |
| 3 |
A、当θ取得最小值时,O′P与OM所成角为
| ||
B、当θ取得最小值时,点P到平面α的距离为
| ||
C、θ的最大值为
| ||
| D、θ的最大值为π |
“a=2”是“l1:ax+4y-1=0与l2:x+ay+3=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
由下列各组命题构成的复合命题中,“p或q”为真命题,“p且q”为假命题,“非p”为真命题的一组为( )
| A、p:3为偶数,q:4为奇数 |
| B、p:π<3,q:5>3 |
| C、p:a∈{a,b},q:{a}?{a,b} |
| D、p:Q?R,q:N=Z |
如图是某一四棱锥的三视图,则这个四棱锥的体积为( )


| A、4 | B、8 | C、16 | D、20 |
已知随机变量X服从正态分布N(1,4),且P(0≤X≤2)=0.68,则P(X>2)=( )
| A、0.34 | B、0.16 |
| C、0.84 | D、0.32 |
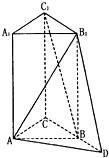 已知正三棱柱ABC-A1B1C1中,AA1=2AC=4,延长CB至D,使CB=BD.
已知正三棱柱ABC-A1B1C1中,AA1=2AC=4,延长CB至D,使CB=BD.