题目内容
5.已知tanα=2,则$\frac{si{n}^{2}α+co{s}^{2}(π-α)}{1+co{s}^{2}α}$的值为$\frac{5}{6}$.分析 利用同角三角函数基本关系式、“弦化切”即可得出.
解答 解:∵tanα=2,
∴$\frac{si{n}^{2}α+co{s}^{2}(π-α)}{1+co{s}^{2}α}$=$\frac{si{n}^{2}α+co{s}^{2}α}{si{n}^{2}α+2co{s}^{2}α}$=$\frac{ta{n}^{2}α+1}{ta{n}^{2}α+2}$=$\frac{{2}^{2}+1}{{2}^{2}+2}$=$\frac{5}{6}$,
故答案为:$\frac{5}{6}$.
点评 本题考查了同角三角函数基本关系式、“弦化切”、诱导公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.若P点是以A(-3,0)、B(3,0)为焦点,实轴长为2$\sqrt{5}$的双曲线与圆x2+y2=9的一个交点,则|PA|+|PB|=( )
| A. | 4$\sqrt{13}$ | B. | 2$\sqrt{14}$ | C. | 2$\sqrt{13}$ | D. | 3$\sqrt{14}$ |
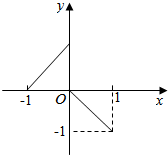 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.