题目内容
16.某毕业班统计全班40名学生报名参加学科竞赛和报名参加自主招生的数据如表:| 报名参加学科竞赛 | 未报名参加学科竞赛 | |
| 报名参加自主招生 | 2 | 4 |
| 未报名参加自主招生 | 6 | 28 |
(2)从报名参加自主招生的同学中任取2人,求恰好1人两项都报名的概率.
分析 (1)根据古典概型的概率计算公式,即可求出对应的概率值;
(2)利用列举法求出对应事件的个数,计算对应的概率值即可.
解答 解:(1)设从该班随机选1名同学,该同学仅报名参加其中一项的事件为A,则P(A)=$\frac{10}{40}$=$\frac{1}{4}$;
(2)设报名参加自主招生的同学中任取2人,恰好1人两项都报名的事件为B,
设参加两项的2名同学分别为a,b,仅参加自主招生的4名同学分别为c,d,e,f;…(6分)
从报名参加自主招生的同学中任取2人有:
ab、ac、ad、ae、af、bc、bd、be、bf、cd、ce、cf、de、df、cf共15种,
其中恰好1人两项都报名的基本事件有:
ac、ad、ae、af、bc、bd、be、bf共8种,
则P(B)=$\frac{8}{15}$;
点评 本题考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
14.函数y=ax3+bx2+cx+d的图象如图所示,则( )


| A. | a>0,b>0,c>0 | B. | a>0,b>0,c<0 | C. | a<0,b<0,c>0 | D. | a<0,b<0,c<0 |
8.不透明袋子中放有大小相同的5个球,球上分别标有号码1,2,3,4,5,若从袋中任取三个球,则这三个球号码之和为5的倍数的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{4}$ |
5.执行如图所示的程序框图,如果输入x=3,则输出k的值为( )


| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
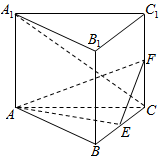 (文科)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,D,E,F分别是AB,BC,CC1的中点.
(文科)如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,D,E,F分别是AB,BC,CC1的中点. 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.