题目内容
 2013年某市某区高考文科数学成绩抽样统计如下表:
2013年某市某区高考文科数学成绩抽样统计如下表:(1)求出表中m、n、M、N的值,并根据表中所给数据在如图所示给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
| 分组 | 频数 | 频率 | 频率/组距 |
| [0,30) | 6 | 0.006 | 0.0002 |
| [30,60) | 82 | 0.082 | 0.0027 |
| [60,90) | 256 | 0.256 | 0.0085 |
| [90,120) | m | n | 0.0145 |
| [120,150] | 220 | N | 0.0073 |
| 合计 | M | 1 |
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有6名学生数学成绩在140分以上,其中男生有4名,要从6名学生中录取2名学生,求其中恰有1名女生被录取的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)根据频率公式求频率、频数及样本容量,根据各小矩形的高作频率分布直方图;
(2)利用样本来估计总体的思想,根据样本中的比例估计总体中90分及90分以上的人数;
(3)写出所有基本事件,从中找出恰有1名女生的基本事件,利用基本事件个数比求概率.
(2)利用样本来估计总体的思想,根据样本中的比例估计总体中90分及90分以上的人数;
(3)写出所有基本事件,从中找出恰有1名女生的基本事件,利用基本事件个数比求概率.
解答:
解:(1)由统计表知:M=
=1000,
m=1000-6-82-256-220=436,
n=
=0.436,N=
=0.220.
频率分布直方图如图:
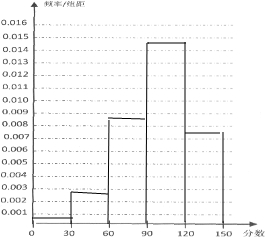
(2)设全市文科数学成绩在90及90分以上的人数为x,
则
=
,x=13120;
(3)设4名男生分别表示为A1、A2、A3、A4,
3名女生分别表示为B1、B2、,
则从6名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),
共8种,故6人中录取2人恰有1人为女生的概率为
.
| 6 |
| 0.006 |
m=1000-6-82-256-220=436,
n=
| 436 |
| 1000 |
| 220 |
| 1000 |
频率分布直方图如图:

(2)设全市文科数学成绩在90及90分以上的人数为x,
则
| 1000 |
| 20000 |
| 656 |
| x |
(3)设4名男生分别表示为A1、A2、A3、A4,
3名女生分别表示为B1、B2、,
则从6名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),
共8种,故6人中录取2人恰有1人为女生的概率为
| 8 |
| 15 |
点评:本题考查了频率分布直方图的作法及利用频率分布直方图求频数,考查了古典概型的概率计算,利用列举法写出所有基本事件是古典概型求概率的常用方法.

练习册系列答案
相关题目
函数f(x)=ln
是定义在(a,b)内的奇函数,则b2+b+a的取值范围为( )
| 1-x |
| 1+x |
| A、[0,1) |
| B、(0,1) |
| C、(0,1] |
| D、[0,1] |
 在正方体ABCD-A1B1C1D1中,E,F分别BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,E,F分别BB1,CD的中点.