题目内容
6.在△ABC中,角A、B、C的对边分别为a、b、c,若$\frac{a}{b}$+$\frac{2b}{a}$=3cosC,则$\frac{sin(A-B)}{sinC}$的值等于3.分析 先利用余弦定理推导出a2=b2+3c2,再由正弦定理推导出$\frac{sin(A-B)}{sinC}$═$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$,由此能求出结果.
解答 解:∵在△ABC中,角A、B、C的对边分别为a、b、c,$\frac{a}{b}$+$\frac{2b}{a}$=3cosC,
∴$\frac{{a}^{2}+2{b}^{2}}{ab}=3×\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
整理,得a2=b2+3c2,
∴$\frac{sin(A-B)}{sinC}$=$\frac{sinAcosB-cosAsinb}{sinc}$
=$\frac{acosB-bcosA}{c}$=$\frac{a•\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}-b•\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}}{c}$
=$\frac{\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2c}-\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2c}}{c}$
=$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$=$\frac{{b}^{2}+3{c}^{2}-{b}^{2}}{{c}^{2}}$
=$\frac{3{c}^{2}}{{c}^{2}}$=3.
故答案为:3.
点评 本题考查三角形中两角差的正弦值与第三个角的正弦值的比值的求法,是中档题,解题时要认真审题,注意正弦定理和余弦定理的合理运用.

练习册系列答案
相关题目
11.已知数列{an}是公比为q(q>0)的等比数列,其中a4=1,且a2,a3,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,求证:Sn<16(n∈N+)
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,求证:Sn<16(n∈N+)
15.函数f(x)在定义域x∈R上,是以5为周期的奇函数,且f(-2)=1,则f(12)等于( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )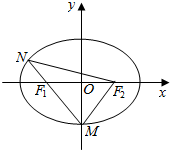 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1、F2分别为椭圆的左、右焦点,M为椭圆的下顶点,直线MF1交椭圆与另一点N.