题目内容
16.已知点O为△ABC内一点,满足$\overrightarrow{OA}+\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$,若$∠AOC=\frac{5π}{6},∠BOC=\frac{3π}{4},OA=4$,则OB=2$\sqrt{2}$.分析 以O为原点,建立平面直角坐标系,设OB=x,OC=y,求出$\overrightarrow{OA}$,$\overrightarrow{OB},\overrightarrow{OC}$的坐标,代入$\overrightarrow{OA}+\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$列出方程组解出.
解答 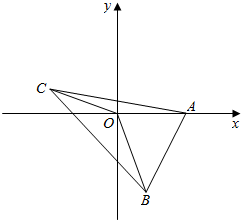 解:以OA为x轴,O为原点建立平面直角坐标系,如图,则∠AOB=$\frac{5π}{12}$,设OB=x,OC=y,则B($\frac{\sqrt{6}-\sqrt{2}}{4}$x,-$\frac{\sqrt{6}+\sqrt{2}}{4}x$),
解:以OA为x轴,O为原点建立平面直角坐标系,如图,则∠AOB=$\frac{5π}{12}$,设OB=x,OC=y,则B($\frac{\sqrt{6}-\sqrt{2}}{4}$x,-$\frac{\sqrt{6}+\sqrt{2}}{4}x$),
C(-$\frac{\sqrt{3}}{2}y$,$\frac{1}{2}y$),A(4,0).∴$\overrightarrow{OA}$=(4,0),$\overrightarrow{OB}$=($\frac{\sqrt{6}-\sqrt{2}}{4}$x,-$\frac{\sqrt{6}+\sqrt{2}}{4}x$),$\overrightarrow{OC}$=(-$\frac{\sqrt{3}}{2}y$,$\frac{1}{2}y$).
∵$\overrightarrow{OA}+\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$,∴$\left\{\begin{array}{l}{4+\frac{\sqrt{6}-\sqrt{2}}{4}x-\frac{3\sqrt{3}}{2}y=0}\\{-\frac{\sqrt{6}+\sqrt{2}}{4}x+\frac{3}{2}y=0}\end{array}\right.$,解得x=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了平面向量在几何中的应用,建立坐标系求出向量坐标是解题关键.

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |