题目内容

7．若命题p：?x∈（0，+∞），x+$\frac{1}{2}$＞2，命题q：?x0∈R，2 x0＜0，则下列为真命题的是（　　）
A．p∧qB．￢p∨qC．p∨qD．￢p∧q

分析 分别判断出p，q的真假，从而判断出复合命题的真假即可．

解答 解：命题p：?x∈（0，+∞），x+$\frac{1}{2}$＞2是假命题，
命题q：?x0∈R，2 x0＜0是真命题，
故￢p∧q是真命题，
故选：D．

点评 本题考查了指数函数的性质，考查复合命题的判断，是一道基础题．

练习册系列答案
相关题目
17．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为4π，且对?x∈R，有f（x）≤f（$\frac{π}{3}$）成立，则f（x）的一个对称中心坐标是（　　）
A．（-$\frac{2π}{3}$，0）B．（-$\frac{π}{3}$，0）C．（$\frac{2π}{3}$，0）D．（$\frac{5π}{3}$，0）
18．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右顶点分别为A，B，右焦点为F，离心率$e=\frac{1}{2}$，点P是椭圆C上异于A，B两点的动点，△APB的面积最大值为$2\sqrt{3}$．
（1）求椭圆C的方程；
（2）若直线AP与直线x=2交于点D，试判断以BD为直径的圆与直线PF的位置关系，并作出证明．
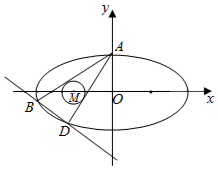15．如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的上顶点为A（0，1），离心率为$\frac{{\sqrt{3}}}{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若过点A作圆M：（x+1）2+y2=r2（0＜r＜1）的两条切线分别与椭圆C相交于点B，D（不同于点A）．当r变化时，试问直线BD是否过某个定点？若是，求出该定点；若不是，请说明理由．
2．已知数列{an}满足a1=1，an+1-2an=2n，
（1）证明：数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列，并求出{an}的通项公式；
（2）设bn=$\frac{（n+2）{2}^{n-1}}{{a}_{n}{a}_{n+1}}$，{bn}的前n项和为Sn，求证：Sn＜1．
12．在△ABC中，若A=30°，B=45°，$BC=\sqrt{6}$，则AC=$2\sqrt{3}$．
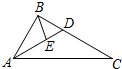19．如图，在△ABC中，已知$∠BAC=\frac{π}{3}$，AB=2，AC=4，点D为边BC上一点，满足$\overrightarrow{AC}$+2$\overrightarrow{AB}$=3$\overrightarrow{AD}$，点E是AD上一点，满足$\overrightarrow{AE}$=2$\overrightarrow{ED}$，则BE=$\frac{2\sqrt{21}}{9}$．
16．已知集合M={x|x2-2x-8≤0}，集合N={x|lgx≥0}，则M∩N=（　　）
A．{x|-2≤x≤4}B．{x|x≥1}C．{x|1≤x≤4}D．{x|x≥-2}
17．运行如图程序，若随机输人一个x值，则输出的结果不可能是（　　）
A．-3B．0C．0.5D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网