题目内容
(本小题满分12分)已知函数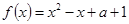
(1)若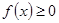 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
(2)求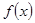 在区间
在区间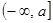 上的最小值
上的最小值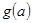 的表达式。
的表达式。
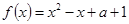
(1)若
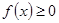 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。(2)求
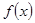 在区间
在区间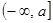 上的最小值
上的最小值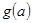 的表达式。
的表达式。(1)
(2)

(2)

试题分析:解:⑴ 由
 对
对 恒成立,即
恒成立,即 恒成立
恒成立∴

∴实数a的取值范围为
 5分
5分⑵ ∵

1°:当
 时,
时,
2°:当
 时,
时, 10分
10分 12分
12分点评:解决的关键是利用函数的最值来得到参数的范围,考查了等价转化思想的运用,属于基础题。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
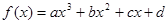
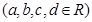 满足:
满足: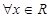 都有
都有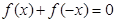 ,且
,且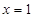 时,
时,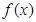 取极小值
取极小值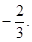
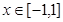 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;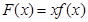 , 当
, 当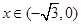 时,求函数
时,求函数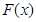 的最小值,并指出当
的最小值,并指出当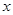 值.
值.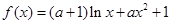 .
.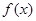 的单调性;
的单调性; 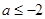 ,证明:对任意
,证明:对任意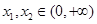 ,
,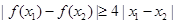 .
.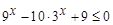 ,求函数
,求函数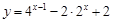 的最大值和最小值;
的最大值和最小值;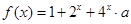 在
在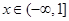 上f (x)
上f (x)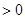 恒成立,求a的取值范围.
恒成立,求a的取值范围.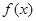 满足:对任意x∈R,都有
满足:对任意x∈R,都有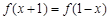 成立,且当
成立,且当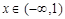 时,
时,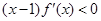 (其中
(其中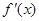 为
为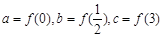 ,则a,b,c三者的大小关系是( )
,则a,b,c三者的大小关系是( )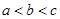
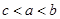
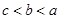
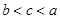
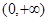 的函数
的函数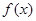 ,对任意的
,对任意的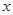 、
、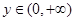 ,都有
,都有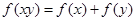 ,且当
,且当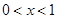 时,
时,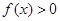 .
.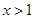 时,
时,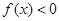 ;
;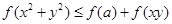 恒成立,求实数
恒成立,求实数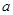 的取值范围.
的取值范围.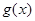 是
是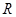 上的奇函数,且当
上的奇函数,且当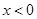 时
时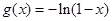 ,函数
,函数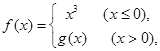 若
若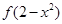 >
>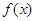 ,则实数
,则实数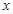 的取值范围是
的取值范围是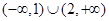
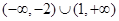

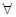 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;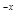 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.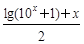 ,h (x)=
,h (x)=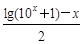
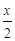 ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)-