题目内容
已知函数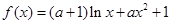 .
.
(Ⅰ)讨论函数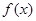 的单调性;
的单调性;
(Ⅱ)设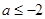 ,证明:对任意
,证明:对任意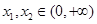 ,
,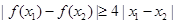 .
.
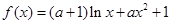 .
.(Ⅰ)讨论函数
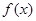 的单调性;
的单调性; (Ⅱ)设
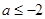 ,证明:对任意
,证明:对任意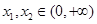 ,
,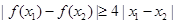 .
.(Ⅰ)分类讨论得到单调性 (Ⅱ)构造函数用导数的方法证明.
试题分析:(Ⅰ) f(x)的定义域为(0,+
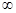 ),
),
当a≥0时,
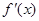 >0,故f(x)在(0,+
>0,故f(x)在(0,+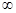 )单调增加;
)单调增加;当a≤-1时,
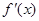 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+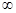 )单调减少;
)单调减少;当-1<a<0时,令
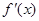 =0,解得x=
=0,解得x=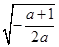 .当x∈(0,
.当x∈(0, 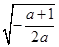 )时,
)时, 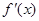 >0;
>0;x∈(
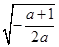 ,+
,+ )时,
)时,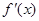 <0, 故f(x)在(0,
<0, 故f(x)在(0, 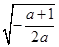 )单调增加,在(
)单调增加,在(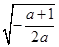 ,+
,+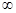 )单调减少
)单调减少 (Ⅱ)不妨设x1≥x2.由于a≤-2,故f(x)在(0,+
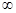 )单调减少.
)单调减少.所以
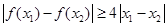 等价于
等价于 ≥4x1-4x2,
≥4x1-4x2,即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则
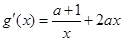 +4=
+4=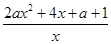 .
. 于是
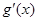 ≤
≤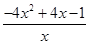 =
=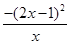 ≤0.
≤0.从而g(x)在(0,+
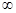 )单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,
)单调减少,故g(x1) ≤g(x2),即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+
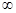 ) ,
) ,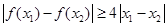 .
.点评:本题考查利用导数研究函数的单调性及函数的最值问题,考查分类讨论思想,考查学生综合运用知识分析问题解决问题的能力,属难题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
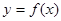 是增函数,且函数
是增函数,且函数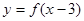 的图像关于(3,0)成中心对称,若
的图像关于(3,0)成中心对称,若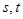 满足不等式
满足不等式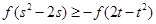 ,当
,当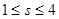 时,则
时,则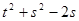 的取值范围为____.
的取值范围为____.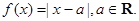
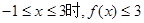 ,求
,求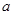 的取值范围;
的取值范围;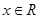 ,
,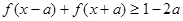 恒成立,求实数
恒成立,求实数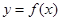 满足:
满足: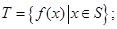 (ii)对任意
(ii)对任意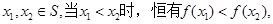
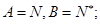
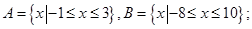
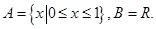
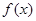 的定义域为R,最小正周期
的定义域为R,最小正周期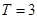 ,若
,若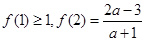 ,则
,则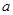 的取值范围是
的取值范围是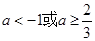
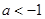
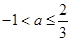
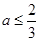
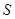 的最大允许值是多少?
的最大允许值是多少?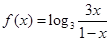 .
. 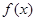 的图像关于点
的图像关于点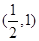 对称;
对称;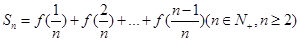 ,求
,求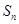 ;
;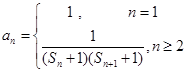
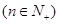 ,
,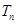 为数列
为数列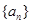 的前
的前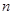 项和,若
项和,若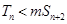 对一切
对一切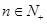 都成立,试求实数
都成立,试求实数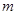 的取值范围.
的取值范围.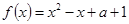
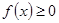 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。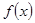 在区间
在区间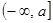 上的最小值
上的最小值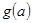 的表达式。
的表达式。