题目内容
18.一盒乒乓球共15个,其中有4个是已用过的,在比赛时,某运动员从中随机取2个使用,比赛结束后又放回盒中,则此盒中已用过的乒乓球个数的所有可能取值.分析 若这两个都为用过的,或者这两个一个是用过的一个是新的,或者这两个都是新的,问题得以解决.
解答 解:一盒乒乓球共15个,其中有4个是已用过的,在比赛时,某运动员从中随机取2个使用,
若这两个都为用过的,或者这两个一个是用过的一个是新的,或者这两个都是新的,
故此盒中已用过的乒乓球个数的所有可能取值4,5,6.
点评 本题考查了简单的分类计数原理,关键是分类,属于基础题.

练习册系列答案
相关题目
13.随机变量X的分布列如下,则m=( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | m | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
18.过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的右焦点F作x轴的垂线,交双曲线于A、B两点,若双曲线的左顶点C在以AB为直径的圆的内部,则此双曲线离心率e的取值范围是( )
| A. | ($\frac{1+\sqrt{5}}{2},+∞$) | B. | ($\frac{1+\sqrt{5}}{2},2$) | C. | (2,+∞) | D. | (1,$\frac{1+\sqrt{5}}{2}$) |
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$以及双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1\;(a>0,b>0)$的渐近线将第一象限三等分,则双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的离心率为( )
| A. | 2或$\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{6}$或$\frac{{2\sqrt{3}}}{3}$ | C. | 2或$\sqrt{3}$ | D. | $\sqrt{3}$或$\sqrt{6}$ |
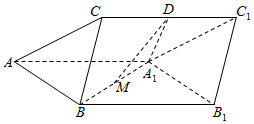 如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,
如图,三棱柱ABC-A1B1C1中,D,M分别为CC1和A1B的中点,A1D⊥CC1,侧面ABB1A1为菱形且∠BAA1=60°,AA1=A1D=2,BC=1,