题目内容
9.设a、b、c是△ABC三条边的长,对任意实数x,f(x)=b2x2+(b2+c2-a2)x+c2,则f(x)与0的大小关系为f(x)>0.分析 由余弦定理可得f(x)=b2x2+2bccosA•x+c2为开口向上的抛物线,由△的符号结合抛物线图象可得.
解答 解:∵a、b、c是△ABC三条边的长,
∴由余弦定理可得b2+c2-a2=2bccosA,
∴f(x)=b2x2+2bccosA•x+c2为开口向上的抛物线,
由△=(2bccosA)2-4b2c2=4b2c2(cos2A-1),
∵A∈(0,π),∴cos2A∈[0,1),
故cos2A-1∈[-1,0),
∴△<0,f(x)>0
故答案为:f(x)>0
点评 本题考查余弦定和二次函数的图象和性质,属基础题.

练习册系列答案
相关题目
14.已知(1+px)(1-x+x2)8的展开式中x4项的系数是42,则p的值是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
10.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线互相垂直,那么此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
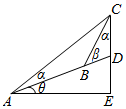 在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.
在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为α,向山顶前进a米到达点B,从B点测得斜度为β,设建筑物的高为h米,山坡对于地平面的倾斜角为θ,则cosθ=$\frac{asinαsinβ}{hsin(β-α)}$.