Question

6．设函数f（x）=$\left\{\begin{array}{l}{|x-10|}，{x≥9}\\{lg（1+x）}，{-1＜x＜9}\end{array}\right.$，若互不相同的实数x₁，x₂，x₃满足f（x₁）=f（x₂）=f（x₃），则x₁+x₂+x₃的取值范围是（20，29）．

Answer 1

分析 作出函数f（x）=|x-10|的图象，令t=f（x₁）=f（x₂）=f（x₃），设x₁＜x₂＜x₃，由图象的对称性可得x₃+x₂=20，作出y=lg（x+1）（x＜9）的图象，由条件可得0＜x₁＜9，即可得到所求范围．

解答 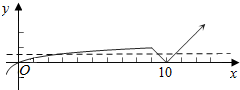解：作出函数f（x）=|x-10|的图象，
令t=f（x₁）=f（x₂）=f（x₃），设x₁＜x₂＜x₃，
则有x₃+x₂=20，
作出y=lg（x+1）（-1＜x＜9）的图象，
若f（x₁）=f（x₂）=f（x₃），则0＜f（x₁）＜1．
由y=1，即有x=9，即0＜x₁＜9，
可得x₁+x₂+x₃的取值范围为（20，29）．
故答案为：（20，29）．

点评 本题考查分段函数的图象和运用，主要考查函数的对称性和对数的运算性质，正确画图和通过图象观察是解题的关键．