题目内容
14.已知正项数列{an}中,a1=l,a2=2,$2a_{n}^2=a_{n+1}^2+a_{n-1}^2$(n≥2),则a6=( )| A. | 16 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 45 |
分析 由题设知an+12-an2=an2-an-12,且数列{an2}为等差数列,首项为1,公差d=a22-a12=3,故an2=1+3(n-1)=3n-2,由此能求出a6.
解答 解:∵正项数列{an}中,a1=1,a2=2,2an2=an+12+an-12(n≥2),
∴an+12-an2=an2-an-12,
∴数列{an2}为等差数列,首项为1,公差d=a22-a12=3,
∴an2=1+3(n-1)=3n-2,
∴an=$\sqrt{3n-2}$
∴a6=$\sqrt{3×6-2}$=4,
故选:B
点评 本题考查了等差数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.直线x+(l-m)y+3=0(m为实数)恒过定点( )
| A. | (3,0) | B. | (0,-3) | C. | (-3,0) | D. | (-3,1) |
2.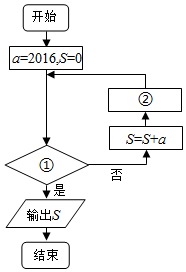 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )| A. | ①a<0?,②a=a-3 | B. | ①a<0?,②a=a+3 | C. | ①a>0?,②a=a-3 | D. | ①a>0?,②a=a+3 |
19.执行如图所示的程序框图,则输出i的值为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 55 |
4.已知直线l与直线2x-y+4=0关于x=1对称,则直线l的方程是( )
| A. | 2x+y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |