题目内容
如图，在四棱锥P-ABCD中，四边形ABCD是平行四边形，AD=AB，PA=PC，AC∩BD=F，点E是PC的中点．（Ⅰ）求证：EF∥平面PAD；
（Ⅱ）求证：平面ADF⊥平面PBD．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（I）利用平行四边形的性质、三角形中位线定理、线面平行的判定定理即可证明；
（II）利用等腰三角形的性质、线面与面面垂直的判定与性质定理即可证明．
（II）利用等腰三角形的性质、线面与面面垂直的判定与性质定理即可证明．
解答：
证明：（I）∵四边形ABCD是平行四边形，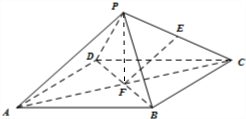
∴F为AC中点，
又∵E为PC中点，∴EF是△PAC的中位线．
∴EF∥PA，而EF?平面PAD内，PA?平面PAD
∴EF∥平面PAD．
（II）连接PF，
∵PA=PC，F为AC中点，
∴PF⊥AF
∵平行四边形ABCD，AD=AB，
∴四边形ABCD是菱形，
∴AF⊥BD，
又∵BD∩PF=F，BD?平面PBD，PF?平面PBD，
∴AF⊥平面PBD，而AF?平面ADF
∴平面ADF⊥平面PBD．
∴F为AC中点，
又∵E为PC中点，∴EF是△PAC的中位线．
∴EF∥PA，而EF?平面PAD内，PA?平面PAD
∴EF∥平面PAD．
（II）连接PF，
∵PA=PC，F为AC中点，
∴PF⊥AF
∵平行四边形ABCD，AD=AB，
∴四边形ABCD是菱形，
∴AF⊥BD，
又∵BD∩PF=F，BD?平面PBD，PF?平面PBD，
∴AF⊥平面PBD，而AF?平面ADF
∴平面ADF⊥平面PBD．
点评：本题考查了平行四边形的性质、三角形中位线定理、线面平行的判定定理、等腰三角形的性质、线面与面面垂直的判定与性质定理，考查了推理能力，属于中档题．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图是利用圆x2+y2=2、函数y=x2及y=-x2的图象得到的．在这个圆内任取一点，则此点落在阴影部分的概率是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某耐磨厂对一批耐磨球的单个重量（单位：克）进行了抽样检测，并绘制出频率分布直方图，已知耐磨球单个重量的范围为[96，106]，样本数据分组为[96，98），[98，100），[100，104），[104，106）
如图，在三棱柱ABC-A1B1C1中，从顶点A1向底面ABC作垂线，垂足O恰好为AC边的中点，四边形A1ACC1为菱形，且∠A1AC=60°，在△ABC中，AB=BC=