题目内容
 如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=
如图,在三棱柱ABC-A1B1C1中,从顶点A1向底面ABC作垂线,垂足O恰好为AC边的中点,四边形A1ACC1为菱形,且∠A1AC=60°,在△ABC中,AB=BC=| 2 |
(Ⅰ)求证:平面A1ACC1⊥平面ABC;
(Ⅱ)求直线A1C与平面A1AB所成角的正弦值;
(Ⅲ)在BC1上是否存在一点E,使得OE∥平面A1AB,若不存在,说明理由;若存在,确定点E的位置.
考点:直线与平面所成的角,直线与平面平行的性质,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由A1O⊥平面ABC,能证明平面A1ACC1⊥平面ABC.
(Ⅱ)连结OB,以O为坐标原点,建立空间直角坐标系,利用向量法能求出直线A1C与平面A1AB所成角的正弦值.
(Ⅲ)设E(x0,y0,z0),
=λ
,得E(1-λ,2λ,
λ),由此利用向量法能求出存在这样的点E,E为BC的中点.
(Ⅱ)连结OB,以O为坐标原点,建立空间直角坐标系,利用向量法能求出直线A1C与平面A1AB所成角的正弦值.
(Ⅲ)设E(x0,y0,z0),
| BE |
| BC1 |
| 3 |
解答:
(Ⅰ)证明:∵A1O⊥平面ABC,A1O?平面AA1C1C,
∴平面A1ACC1⊥平面ABC.
(Ⅱ)解:连结OB,由题意得A1O⊥OC,A1O⊥OB,OB⊥OC,
以O为坐标原点,建立空间直角坐标系,
∵AB=BC=
,AB⊥BC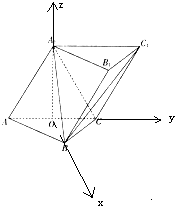
∴AC=2,OB=
AC=1,
又∵四边形A1ACC1为菱形,∠A1AC=60°,
∴A1A=A1C=AC=2,
∴O(0,0,0),A(0,-1,0),A1(0,0,
),
C(0,1,0),C1(0,2,
),B(1,0,0),
∴
=(0,1,-
),
=(0,1,
),
=(1,1,0),
设平面AA1B的一个法向量为
=(x,y,z),
则
,取x=-1,得
=(-1,1,-
),
∴cos<
,
>=
=
,
∵直线A1C与平面A1AB所成角与<
,
>互余,
∴直线A1C与平面A1AB所成角的正弦值为
.
(Ⅲ)解:设E(x0,y0,z0),
=λ
,
即(x0-1,y0,z0)=λ(-1,2,
),
得
,∴E(1-λ,2λ,
λ),
∴
=(1-λ,2λ,
λ),
令OE∥平面A1AB,得
•
=0,
∴-(1-λ)+2λ-λ=0,解得λ=
,
即存在这样的点E,E为BC的中点.
∴平面A1ACC1⊥平面ABC.
(Ⅱ)解:连结OB,由题意得A1O⊥OC,A1O⊥OB,OB⊥OC,
以O为坐标原点,建立空间直角坐标系,
∵AB=BC=
| 2 |

∴AC=2,OB=
| 1 |
| 2 |
又∵四边形A1ACC1为菱形,∠A1AC=60°,
∴A1A=A1C=AC=2,
∴O(0,0,0),A(0,-1,0),A1(0,0,
| 3 |
C(0,1,0),C1(0,2,
| 3 |
∴
| A1C |
| 3 |
| AA1 |
| 3 |
| AB |
设平面AA1B的一个法向量为
| n |
则
|
| n |
| ||
| 3 |
∴cos<
| n |
| A1C |
1+
| ||||
2
|
| ||
| 7 |
∵直线A1C与平面A1AB所成角与<
| n |
| A1C |
∴直线A1C与平面A1AB所成角的正弦值为
| ||
| 7 |
(Ⅲ)解:设E(x0,y0,z0),
| BE |
| BC1 |
即(x0-1,y0,z0)=λ(-1,2,
| 3 |
得
|
| 3 |
∴
| OE |
| 3 |
令OE∥平面A1AB,得
| OE |
| n |
∴-(1-λ)+2λ-λ=0,解得λ=
| 1 |
| 2 |
即存在这样的点E,E为BC的中点.
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法,考查满足条件的点是否存在的判断与求法,解题时要注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD=AB,PA=PC,AC∩BD=F,点E是PC的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,AD=AB,PA=PC,AC∩BD=F,点E是PC的中点.

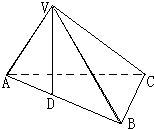 如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.
如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.